Лекция 1: «Множество. Алгебра множеств»

Введем обозначения:

N(или ω) –множество натуральных чисел;

Z– множество целых чисел;

Q– множество рациональных чисел;

R – множество действительных (вещественных) чисел;

С – множество комплексных чисел.

X R – элемент X принадлежит множеству R.

Равные множества – множества, состоящие из одинаковых элементов.

A = B – множество А равно множеству B.

Ø – пустое множество.

AC – Множество А является подмножеством множества С.

Если ACиA C, тоA C(строго).

Если A C и C A, тоA= С.

Пустое множество Ø является подмножеством любого множества.

Универсальное множество (универсум) Uсодержит в себе все множества и любое множество является подмножеством универсального множества.

Можно записать следующее: ØNZQRCU.

Множества A и B называются эквивалентными (обозначается A~B), если биекция f: A↔B (или по другому y=f(x) и x=f(y), при yA и xB).

МощностьюмножестваAназывается класс всех множеств, эквивалентных множествуA(обозначается ).

Существуют конечные и бесконечные множества. Пусть множество Aсостоит изnэлементов. Это множество называется конечным. Числоnназывается мощностью данного множества. =n.

Множество натуральных чисел мощность является счетным (т.е. все элементы можно пронумеровать). Если A~N, то мощность =N.

Если A~, т.е. A={1,2,4,8,…, ,…}, то множество A называется континуальным (или континуумом). Мощность .

Основное правило комбинаторики (показано на примере)

Пусть имеется палочка, разделенная на 3 части. Первую ее часть можно раскрасить n способами, вторую – m, третью – k. Всего способов раскраски палочки – n*m*k.

Аналогично с множествами

U = {a₁,a₂… a_n-1, a_n}

Пусть U = {a₁, a₂, a₃}

Выпишем множество всех подмножеств множества U.

P(U) = {0, a1, a2, a3, a1a2, a1a3, a2a3, a1a2a3}.

Мощность множества U равна 3, а мощность P(U) равна 8.

Методом математической индукции доказывается, что при произвольной мощности n множества U, мощность множества P(U) равна 2ⁿ.

Операции над множествами

1. Объединение множеств (AB). Элемент, принадлежащий полученному множеству, принадлежит множествуAИЛИ множеству В.

2. Пересечение множеств (AB). Элемент, принадлежащий полученному множеству, принадлежит множествуAи множеству В.

3. Дополнение множества А. (С = ) – не А. Все элементы, принадлежащие универсальному множеству, не принадлежащие множеству А.

Свойства операций над множествами

1. A B = B A; AB = BA – коммутативность.

2. (AB)C =A(BC), A(BC)=(AB)C – ассоциативность.

3. (AB)C = (AC)(BC), (AB)C=(AC)(BC) – дистрибутивность.

4. Поглощение A A = A, A A = A.

5. Существование универсальных границ.

А Ø = A; A Ø = Ø; A U = U; A U = A

6. Двойное дополнение

7. Ø

8. Законы двойственности или закон Де – Моргана

Пересечение множеств

Объединение множеств

Дополнение множества

Лекция 2: «Теория булевых функций. Булева алгебра»

Определение: Множество M с двумя введенными бинарными операциями (& V), одной унарной операцией () и двумя выделенными элементами называетсябулевой алгеброй, если выполнены следующие свойства (аксиомы булевой алгебры). Названия операций пока не введены.

1. X & Y = Y&X, X V Y = Y V X – коммутативность.

2. (X & Y) & Z = X & (Y & Z), (X V Y) V Z = X V (Y V Z) – ассоциативность.

3. (X V Y) & Z = (X & Z) V (Y & Z), (X & Y) V (Y & Z) = (X V Z) & (Y & Z) – дистрибутивность.

4. Поглощение – X & X = X, X V X = X.

5. Свойства констант

X & 0 = 0

X & I = X, где I – аналог универсального множества.

6. Инвальтивность (двойное отрицание) .

7. Дополнимость X V 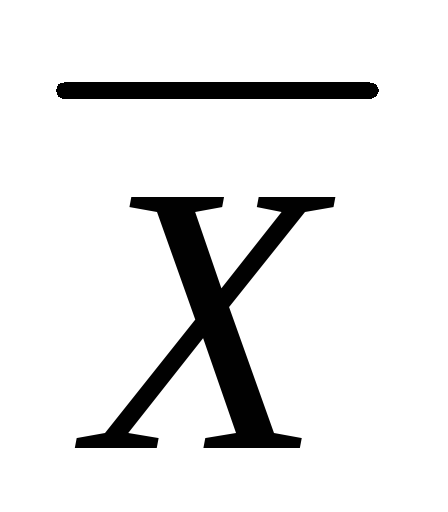= I, X & = 0.

8. Законы двойственности – (X & Y)* = X* V Y*, (X V Y)* = X* & Y

Булева алгебра всех подмножеств данного множества.

U = {a1, a2… an)

[U] = N

[P(U)] = 2ⁿ

Легко показать, что свойства операций над множествами совпадают со свойствами (аксиомами) булевой алгебры. То есть, множество P(U) с операциями объединения, пересечения и дополнения является булевой алгеброй.

Oбъединение эквивалентно V, пересечение - &, дополнение - , пустое множество – 0, а универсальное – I.

Все аксиомы булевой алгебры справедливы в операциях над множествами.