Статистический анализ таблицы сопряженности двух порядковых признаков

Если таблица основана на двух переменных, каждая из которых имеет порядковый уровень измерения, используется коэффициент корреляции Кэнделла (tau-b), который может принимать значения от –1 до +1.

(3)

сумма произведений внутриклеточных частот на сумму частот, расположенных ниже и правее данной клетки.

— сумма произведений внутриклеточных частот на сумму частот, расположенных ниже и левее данной клетки;

сумма произведений внутриклеточных частот на сумму частот, расположенных в данной строке правее данной клетки

сумма произведений частот, расположенных в данном столбце ниже данной клетки.

Знак коэффициента указывает на направление — прямое или обратное —данной связи. Отрицательный знак говорит об обратной связи, положительный — о прямой. Так, например, если политологу известно, что значимый коэффициент корреляции между возрастом и стажем политика составил +0,64, то это говорит о том, что с увеличением возраста стаж тоже растет. Если бы знак был отрицательный, то следовало бы сказать, что с увеличением возраста стаж уменьшается.

Таблица 10

Влияние оценки изменения материального положения семьи на отношение к политику N

Оценка изменения материального положения семьи за последний год	Отношение к политику N
	Положительное	Нейтральное	Отрицательное
Улучшилось	89	42	19	150
	59,3%	28,0%	12,7%	100%
Осталось без изменений	46	52	25	123
	37,4%	42,3%	20,3%	100%
Ухудшилось	20	38	42	100
	20,0%	38,0%	42,0%	100%

Рассмотрим данные, приведённые в таблице 10. Оценку изменения материального положения семьи будем считать независимой, а отношение к политику N —зависимой переменной. Обратим внимание на то, что порядок значений признаков, положенных в основу таблицы, должен быть одинаковым. В данном случае этот порядок—от большего к меньшему.

Нулевая гипотеза в нашем случае — предположение, что степень выраженности позитивного отношения к политику N не зависит от оценки изменения материального положения семьи. Рассчитаем для нашей таблицы.

S=89(52+25+38+42)+42(25+42)+46(38+42)+52(42)=22651

D=19(46+52+20+38)+25(20+38)+42(46+20)+52(20)=8226

89(42+19)+42(19)+46(52+25)+52(25)+20(38+42)+38(42)=14265

89(46+20)+46(20)+42(52+38)+52(38)+19(25+42)+25(42)=14873

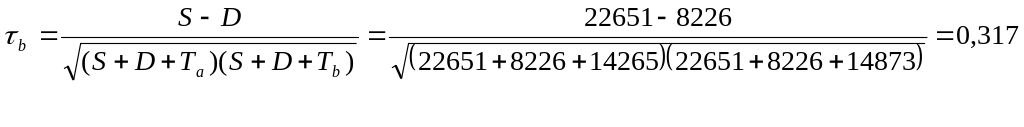Значимость данного коэффициента проверяется с помощью Z-критерия

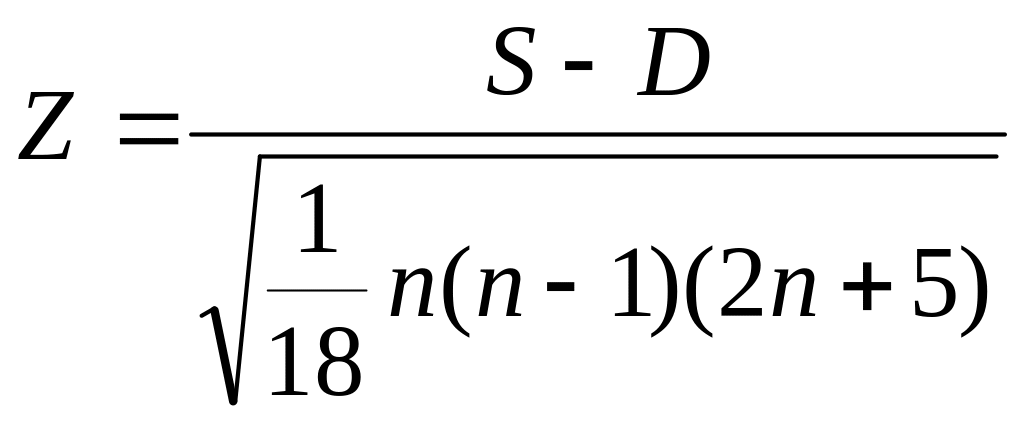(4)

Е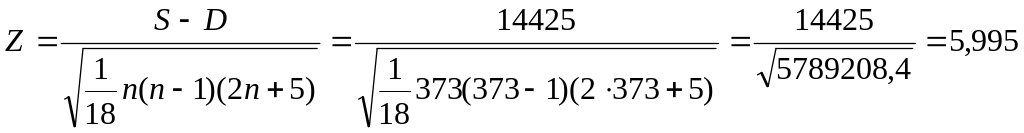 сли расчётное значение Z-критерия превышает критическое, определяемое по таблицам нормального распределения, то связь является статистически значимой. Для доверительной вероятности 0,95 критическое значение данного критерия составляет 1,96.¹ Так как 5,995 , коэффициент значим.

Убедившись в том, что коэффициент Кендалла значим и имеет знак “+” можно сделать следующий вывод из данных, приведенных в таблице.

Чем лучше оценка материального положения семьи по сравнению с прошлым годом, тем лучше отношение к политику N. Так, среди улучшивших материальное положение положительно относятся к данному политику 59,3%, в группе не изменивших материальное положение данный показатель снижается до 37,4%, а среди ухудшивших он составляет всего 20%.

Если бы коэффициент оказался отрицательным, следовало бы сделать следующий вывод: «Чем лучше оценка материального положения семьи по сравнению с прошлым годом, тем хуже отношение к политику N.»

1 Более математически обосновано независимая переменная определяется как признак, на основе значений которого могут быть предсказаны значения другого признака

1 Техника расчёта значения данного критерия приведена практически во всех учебных пособиях, затрагивающих проблему анализа данных, например, Мангейм Д., Рич Р. Политология. Методы исследований. М., 1997. С.422.

1 Таблицы значений интеграла вероятностей нормального закона распределения см. Общая теория статистики. М.:Финансы и статистика, 1996. С.290.