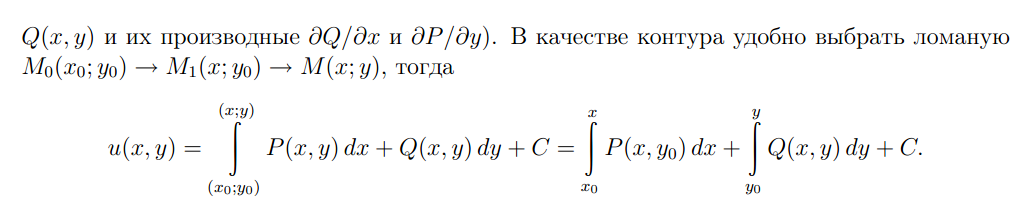- •Математический анилиз Линии и поверхности
- •Интегралы Определения
- •Параметрическая форма
- •Свойства
- •Поверхностный интеграл второго рода Определение
- •Связь между поверхностными интегралами второго и первого рода
- •Свойства
- •Определитель Грама Геометрический смысл определителя Грама
- •Скалярное поле
- •Операции
- •Теорема о вычислении криволинейного интеграла второго рода в r3
- •Теорема о вычислении поверхностного интеграла второго рода
- •Теорема Гаусса – Остроградского в r3
- •Формула Кельвина — Стокса
- •Независимость криволинейного интеграла от пути.
- •Интегрирование полных дифференциалов. Общая теорема стокса об интегрировании внешних форм.
Скалярное поле
Если каждой точке M некоторой области некоторого пространства (чаще всего подразумевается, что размерность этого пространства больше единицы) поставлено в соответствие некоторое (обычно — действительное) число u, то говорят, что в этой области задано скалярное поле. Другими словами, скалярное поле — это функция, отображающая Rn в R (скалярная функция точки пространства). Точка пространства при этом на практике может быть указана или просто символически, или с помощью вектора (если пространство может быть представлено как векторное) или набором координат.
Векторое поле Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Например, вектор скорости ветра в данный момент времени изменяется от точки к точке и может быть описан векторным полем.
Операции
Градиент
Для
случая трёхмерного пространства
градиентом скалярной функции
![]() координат
координат
![]() ,
,
![]() ,
,
![]() называется
векторная функция с компонентами
называется
векторная функция с компонентами
![]() ,
,
![]() ,
,
![]() .
.
Дивергенция
![]()
где ФF — поток векторного поля F через сферическую поверхность площадью S, ограничивающую объём V. Ещё более общим, а потому удобным в применении, является определение, когда форма области с поверхностью S и объёмом V допускается любой. Единственным требованием является её нахождение внутри сферы радиусом, стремящимся к нулю (то есть чтобы вся поверхность находилась в бесконечно малой окрестности данной точки, что нужно, чтобы дивергенция была локальной операцией и для чего очевидно недостаточно стремления к нулю площади поверхности и объёма ее внутренности). В обоих случаях подразумевается, что
 .
.
Допустим, что векторное поле дифференцируемо в некоторой области. Тогда в трёхмерном декартовом пространстве дивергенция будет определяться выражением
![]()
Это же выражение можно записать с использованием оператора набла
![]()
Многомерная, а также двумерная и одномерная, дивергенция определяется в декартовых координатах в пространствах соответствующей размерности совершенно аналогично (в верхней формуле меняется лишь количество слагаемых, а нижняя остается той же, подразумевая оператор набла подходящей размерности).
Ротор
Ротор
![]() векторного
поля
векторного
поля ![]() — есть вектор, проекция которого
— есть вектор, проекция которого
![]() на
каждое направление n
есть предел отношения циркуляции
векторного поля
по контуру L,
являющемуся краем плоской площадки ΔS,
перпендикулярной этому направлению, к
величине этой площадки, когда размеры
площадки стремятся к нулю, а сама площадка
стягивается в точку:
на
каждое направление n
есть предел отношения циркуляции
векторного поля
по контуру L,
являющемуся краем плоской площадки ΔS,
перпендикулярной этому направлению, к
величине этой площадки, когда размеры
площадки стремятся к нулю, а сама площадка
стягивается в точку:
 .
.
Направление обхода контура выбирается так, чтобы, если смотреть в направлении , контур L обходился по часовой стрелке[4].
В
трёхмерной декартовой системе координат
ротор (в соответствии с определением
выше) вычисляется следующим образом
(здесь F
- обозначено некое векторное поле с
декартовыми компонентами
![]() ,
а
,
а
![]() -
орты
декартовых координат):
-
орты
декартовых координат):
![]()
![]()
![]()
или
![]()
![]()
![]()
Оператор Гамильтона
Опера́тор на́бла (оператор
Гамильтона) — векторный
дифференциальный
оператор, обозначаемый символом
![]() (набла)
(в Юникоде
U+2207,
∇). Для
трёхмерного евклидова
пространства в
прямоугольных
декартовых
координатах[1]
оператор набла определяется следующим
образом:
(набла)
(в Юникоде
U+2207,
∇). Для
трёхмерного евклидова
пространства в
прямоугольных
декартовых
координатах[1]
оператор набла определяется следующим
образом:
![]() ,
,
где
![]() —
единичные векторы по осям x, y,
z.
—
единичные векторы по осям x, y,
z.
Оператор Лапласа.
Опера́тор
Лапла́са
(лапласиа́н,
оператор дельта) — дифференциальный
оператор, действующий в линейном
пространстве гладких функций и
обозначаемый символом
![]() .
Функции
.
Функции
![]() он
ставит в соответствие функцию
он
ставит в соответствие функцию
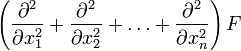 .
.
Оператор
Лапласа эквивалентен последовательному
взятию операций градиента
и дивергенции:
![]() ,
таким образом, значение оператора
Лапласа в точке может быть истолковано
как плотность источников (стоков)
потенциального
векторного поля
,
таким образом, значение оператора
Лапласа в точке может быть истолковано
как плотность источников (стоков)
потенциального
векторного поля
![]() в
этой точке. В декартовой системе координат
оператор Лапласа часто обозначается
следующим образом
в
этой точке. В декартовой системе координат
оператор Лапласа часто обозначается
следующим образом
![]() ,
то есть в виде скалярного произведения
оператора
набла
на себя. Оператор Лапласа унитарен.
,
то есть в виде скалярного произведения
оператора
набла
на себя. Оператор Лапласа унитарен.
Длина кривой (дуги кривой) – это предел, к которому стремятся длины вписанных в эту кривую (дугу) ломаных при неограниченном увеличении числа их звеньев, когда длина наибольшего звена стремится к нулю.
Определение.
Если
множество ![]() длин вписанных в кривую L ломаных,
отвечающих всевозможным разбиением Т
[
длин вписанных в кривую L ломаных,
отвечающих всевозможным разбиением Т
[![]() ,
, ![]() ]
ограничено, то кривая L называется
спрямляемой.
Точная
верхняя грань l множества
называется длиной
дуги кривой L.
]
ограничено, то кривая L называется
спрямляемой.
Точная
верхняя грань l множества
называется длиной
дуги кривой L.
Площадь поверхностей
Проще всего определяется площадь многогранных поверхностей: как сумма площадей их плоских граней.
Чаще всего площадь поверхности определяют для класса кусочно гладких поверхностей с кусочно гладким краем (или без края). Обычно это делают с помощью следующей конструкции. Поверхность разбивают на мелкие части с кусочно гладкими границами: в каждой части выбирают точку, в которой существует касательная плоскость, и ортогонально проектируют рассматриваемую часть на касательную плоскость поверхности в выбранной точке; площадь полученных плоских проекций суммируют; наконец, переходят к пределу при всё более мелких разбиениях (таких, что наибольший из диаметров частей разбиения стремится к нулю). На указанном классе поверхностей этот предел всегда существует,
Потенциальное векторное поле – поле где ротор равен нулю.
Векторное поле называется соленоидальным, если через любую замкнутую поверхность S его поток равен нулю:
![]() .
.
Если
это условие выполняется для любых
замкнутых S
в некоторой области (по умолчанию -
всюду), то это условие равносильно тому,
что равна нулю дивергенция
векторного поля
![]() :
:
![]()
Критерий спрямляемости
Линия спрямляема тогда и только тогда когда функция которая ее задает – функция с ограниченой вариацией.

Критерий Дарбу.
Особо
не меняется просто находим нижние и
верхние суммы Дарбу

Где mi-точная нижняя грань функции вдоль линии, Mi-точная верхняя грань функции вдоль линии

Переходим
к пределу:  =
= <=> существует
<=> существует

Теорема о вычислении криволинейного интеграла
если L- кусочно-гладкая кривая.
Функция f(x)- кусочнo-непрерывна вдоль кривой L То существует криволинейный интеграл первого рода и справедливо равенство.
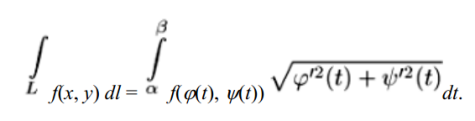
Теорема о вычислении поверхностных интегралов первого рода.
 g11=
g11=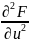 g22=
g22=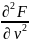 g12=
g12=
Криволинейные интегралы 2-го роды в R2
Вычисление


Формула Грина
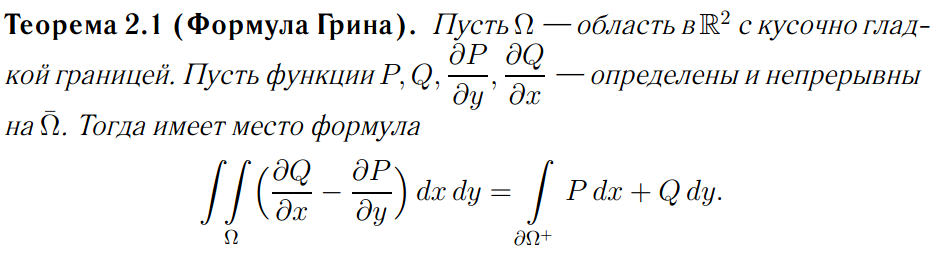
Независимость интеграла от пути.
Пусть в области D заданы непрерывные функции P(x,y) и Q(х,y) и M0M - гладкая дуга, лежащая в области D.
Рассмотрим вопрос о независимости интеграла

от формы пути интегрирования. Имеет место следующая теорема.
Теорема 3.3. Пусть функции P, Q, P'y, Q'x определены и непрерывны в односвязной, ограниченной замкнутой области D плоскости Оху. Тогда следующие четыре условия равносильны между собой: 1)
![]()
, где L - замкнутый контур в области D; 2) интеграл
не зависит от формы пути интегрирования, а зависит лишь от положения точек M0 и М; 3) Pdx + Qdy = dU - полный дифференциал некоторой функции U(x,y); 4)

в каждой точке области D.
Идея
доказательства этой теоремы: показывается,
что из условия 1
![]() условие
2
условие
3
условие
4
условие
1.
условие
2
условие
3
условие
4
условие
1.
Интегрирование полных дифференциалов
Предположим, что выражение![]() есть
полный дифференциал функции
есть
полный дифференциал функции![]() .
В соответствии с доказательствами
условий независимости криволинейного
интеграла
.
В соответствии с доказательствами
условий независимости криволинейного
интеграла![]() от
выбора пути
от
выбора пути![]() можно
заключить, что большое количество
функций, которые удовлетворяют
условию
можно
заключить, что большое количество
функций, которые удовлетворяют
условию![]() представляют
собой
представляют
собой
![]()
Для того, чтобы определить функцию
,
за путь интегрирования можно принять,
допустим,![]() ,
здесь
,
здесь![]() и
и![]() представлены
в качестве отрезков, которые являются
параллельными осям координат (рис.
26.7). В этом случае
представлены
в качестве отрезков, которые являются
параллельными осям координат (рис.
26.7). В этом случае
![]()
Учитывая то, что
![]()
имеем
(26.6)
![]()
Восстановление функции по ее полному дифференциалу.