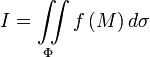Математический анилиз Линии и поверхности

Линия в R² Уравнением линии (или кривой) на плоскости Оху называется такое уравнение F(x;y) = 0 с двумя переменными(явно, не явно), которому удовлетворяют координаты  x и у  каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии Линию на плоскости можно задать при помощи двух уравнений (Параметрически):

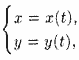
Иначе говоря – линия в R² – множество точек которое удовлетворяет уравнению с двумя переменными в явном или не явном виде или может быть задано параметрически. В R³ множество точек может быть задано параметрически или пересечением двух поверхностей.

В Rⁿ Задается параметрически

Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение F(x, у, z) = 0 с тремя переменны­ми х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности.

В Rⁿ Задается параметрически

К поверхность в Rⁿ К≥1 K≤n Q^К – множество точек из Rⁿ Q^K={x∈Rⁿ : x=x(t) , t∈D_t<R^K}

Ориентируемая поверхность – поверхность которая может быть ориентирована.

Интегралы Определения

Пусть  — гладкая, без особых точек и самопересечений кривая (допускается одно самопересечение — случай замкнутой кривой), заданная параметрически.

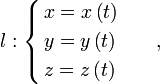
- (отрезок параметризации) — рассматриваем часть кривой.

Пусть  — разбиение отрезка параметризации , причем .

Зададим разбиение кривой .

За обозначим часть кривой от точки до точки , .

Введем мелкость разбиения отрезка параметризации : .

Введем набор промежуточных точек разбиения отрезка параметризации : .

Зададим набор промежуточных точек разбиения кривой .

Пусть нам также даны 4 функции, которые определены вдоль кривой : , , , .

Рассмотрим 4 интегральные суммы.

1) Интегральная сумма криволинейного интеграла первого рода:

.

2) Три интегральных суммы криволинейного интеграла второго рода:

,

,

.

Если , то говорят, что функция интегрируема в смысле криволинейного интеграла первого рода по кривой , а сам предел называют криволинейным интегралом первого рода функции по кривой и обозначают . Здесь  — дифференциал кривой.

Если , , , то говорят, что функции , и интегрируемы в смысле криволинейного интеграла второго рода по кривой , а сами пределы называют криволинейными интегралами второго рода функций , и по кривой и обозначают

Сумму криволинейных интегралов второго рода функций , и также называют криволинейным интегралом второго рода вектор-функции и обозначают:

.

Если кривая замкнута (начало совпадает с концом), то в этом случае вместо значка принято писать .

Криволинейный интеграл первого рода

Свойства

1. Линейность:

2. Аддитивность: если в одной точке, то

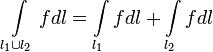
3. Монотонность: если на , то

4. Теорема о среднем для непрерывной вдоль функции :

Очевидно, что: .

5. Изменение направления обхода кривой интегрирования не влияет на знак интеграла: .

6. Криволинейный интеграл первого рода не зависит от параметризации кривой.

Вычисление

Пусть  — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция определена и интегрируема вдоль кривой в смысле криволинейного интеграла первого рода. Тогда

.

Здесь точкой обозначена производная по : .

Криволинейный интеграл второго рода

Свойства

1. Линейность:

2. Аддитивность:

3. Монотонность: если на , то

4. Оценка модуля:

5. Теорема о среднем: если непрерывна на , то , такая что: 6.

Вычисление

Пусть  — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция определена и интегрируема вдоль кривой в смысле криволинейного интеграла второго рода. Тогда

,

,

.

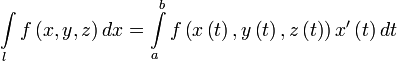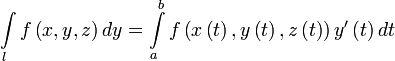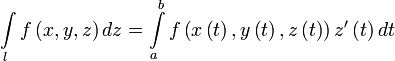Если обозначить за единичный вектор касательной к кривой , то нетрудно показать, что

Взаимосвязь криволинейных интегралов

Пусть  — гладкая, спрямляемая кривая, заданная параметрически (как в определении),  — единичный вектор, касательный к кривой . Пусть также координаты вектор-функции определены и интегрируемы вдоль кривой в смысле криволинейного интеграла второго рода. Тогда

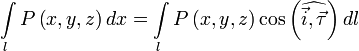
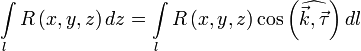
Поверхностный интеграл первого рода

Определение

Пусть  — гладкая, ограниченная полная поверхность. Пусть далее на задана функция . Рассмотрим разбиение этой поверхности на части кусочно-гладкими кривыми и на каждой такой части выберем произвольную точку . Вычислив значение функции в этой точке и, приняв за  — площадь поверхности рассмотрим сумму .

Тогда число называется пределом сумм , если:

Предел сумм при называется поверхностным интегралом первого рода от функции по поверхности и обозначается следующим образом: