Раздел 3.2 Численные методы алгебры
Задание 3.2.1
Решить СЛАУ:
а) методом LU – разложения;
б) методом Холесского (методом квадратного корня).
Все промежуточные вычисления проводить с точностью до трех знаков после запятой (если округление дает ноль, то учесть первую значащую цифру), а ответы округлить до двух знаков после запятой.
Вариант 1 Вариант 2
Вариант 3 Вариант 4
Вариант 5 Вариант 6
Вариант 7 Вариант 8
Вариант 9 Вариант 10
Задание 3.2.2
Решить СЛАУ
итерационными методами, приняв
и взяв три итерации:
а) методом Зейделя;
б) методом итераций с чебышевским набором параметром;
в) методом минимальных невязок;
г) методом наискорейшего спуска.
Все промежуточные вычисления проводить с точностью до трех знаков после запятой (если округление дает ноль, то учесть первую значащую цифру), а ответы округлить до двух знаков после запятой.
Вариант 1 Вариант 2 Вариант 3 Вариант 4
Вариант 5 Вариант 6 Вариант 7 Вариант 8
Вариант 9 Вариант 10
Раздел 3.3 Численные методы анализа
Задание 3.3.1
Составить интерполяционный многочлен Лагранжа для функции, заданной таблицей.
Вариант 1 Вариант 2
Вариант 3 Вариант 4
Вариант 5 Вариант 6
Вариант 7 Вариант 8
Вариант 9 Вариант 10
Задание 3.3.2
Используя первую
интерполяционную формулу Ньютона,
составить интерполяционный многочлен
Ньютона для функции заданной таблицей
и, пользуясь им, найти значение
при
.
Вариант 1 Вариант 2
Вариант 3 Вариант 4
Вариант 5 Вариант 6
Вариант 7 Вариант 8
Вариант 9 Вариант 10
Задание 3.3.3
Разбив интервал
интегрирования на 10 равных частей,
вычислить приближенное значение
определенного интеграла
:
а) по формуле прямоугольников;
б) по формуле трапеций;
в) по формуле Симпсона.
Вычислить относительную погрешность полученных результатов, найдя точное значение интеграла по формуле Ньютона – Лейбница.
Все промежуточные вычисления проводить с точностью до трех знаков после запятой (если округление дает ноль, то учесть первую значащую цифру), а ответы округлить до двух знаков после запятой.
Вариант 1 
. Вариант
2 
.
Вариант 3 
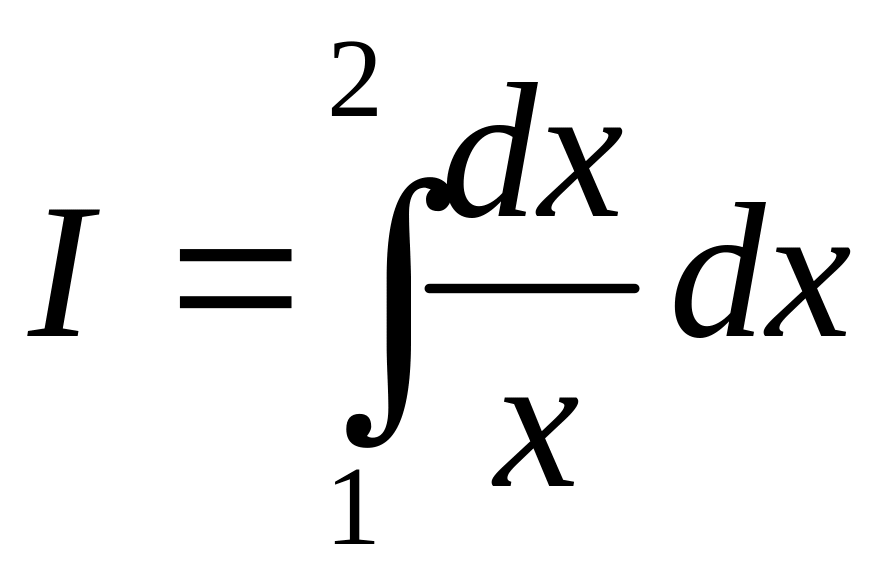. Вариант
4 
.
Вариант 5 
Вариант
6 
.
Вариант 7 
. Вариант
8 
.
Вариант 9 
. Вариант
10 
.
Задание 3.3.4
Методом касательных (методом Ньютона) найти положительный корень уравнения с точностью до 0,01.
Все промежуточные вычисления проводить с точностью до трех знаков после запятой (если округление дает ноль, то учесть первую значащую цифру).
Вариант 1 
. Вариант
2
.
Вариант 3 
. Вариант
4
.
Вариант 5 
. Вариант
6
.
Вариант 7 
. Вариант
8
.
Вариант 9 
. Вариант
10
.
Раздел 3.4 Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений
Задание 3.4.1
Методом ломанных
Эйлера найти приближенное решение
задачи Коши, определив четыре значения
функции
,
определяемой уравнением
,
при начальном
условии
.
Шаг
изменения аргумента
взять равным 0,1.
Все промежуточные вычисления проводить с точностью до трех знаков после запятой (если округление дает ноль, то учесть первую значащую цифру), а ответы округлить до двух знаков после запятой.
Вариант 1 
, 
.
Вариант 2 
,
.
Вариант 3 
, 
.
Вариант 4 
,
.
Вариант 5 
,
.
Вариант 6 
,
.
Вариант 7 , .
Вариант 8 
,
.
Вариант 9 
,
.
Вариант 10 
,
.
Задание 3.4.2
Методом Рунге Кутта четвертого порядка точности найти на отрезке приближенное решение задачи Коши: , . Шаг изменения аргумента взять равным 0,2.
Все промежуточные вычисления проводить с точностью до трех знаков после запятой (если округление дает ноль, то учесть первую значащую цифру), а ответы округлить до двух знаков после запятой.
Вариант |
|
|
|
|
|
1 |
|
1 |
1 |
1 |
2 |
2 |
|
1 |
1 |
1 |
2 |
3 |
|
0 |
0 |
0 |
1 |
4 |
|
0 |
1 |
0 |
1 |
5 |
|
1 |
0 |
1 |
2 |
6 |
|
1 |
0 |
1 |
2 |
7 |
|
1 |
0 |
1 |
2 |
8 |
|
1 |
|
1 |
2 |
9 |
|
1 |
2 |
1 |
2 |
10 |
|
1 |
0 |
1 |
2 |
