2.Билет

Классическое определение вероятности событий: оно основывается на понятии равновозможности появления одного из n исходов при проведении опыта. Если в результате проведения опыта может произойти n исходов, а некоторому событию благоприятствует исходов, то вероятность данного события определяется по формул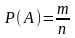е: где – вероятность;( ) – записывается событие, ( ) – рассматривается событие ; – число возможных исходов; – число благоприятных исходов.

Вероятность определяется ещё до опыта.

Статистическое определение вероятности: классическое определение вероятностей при переходе от простейших примеров к сложным становится неприменимым, так как во многих случаях не представляется возможным обосновать равновозможность всех исходов, которые могут произойти в результате проведения опыта. В этом случае вероятность события определяется по статистической схеме. Проводится n независимых опытов, определяется число опытов , при которых появляется событие , и статистическая вероятность определяется по формуле:

Геометрическая вероятность: с начала развития теории вероятностей были замечены недостатки как классического, так и статистического определения вероятности события. Это возникало в тех случаях, когда число возможных исходов при проведении опыта было равно бесконечности и число благоприятных исходов равнялось бесконечности. Поэтому было введено такое понятие как геометрическая вероятность.

Пусть множество М является возможными исходами. При этом данное множество является подмножеством либо числовой оси R (множество чисел), либо квадрата R² (плоскость), либо R³ (объём) и т.д.

Для решения вероятностей задачи вводится понятие меры некоторого события А: (А) ("мю"). Под мерой события А может пониматься длина, площадь и т.д. Наряду с этой мерой вводится мера множества М - (М). Тогда геометрическая вероятность события А определяется по формуле:

Для того чтобы все эти понятия объединить в единое понятие, Колмогоров разработал аксиоматическое построение теории вероятности.

Основные аксиомы теории вероятностей:

1. Каждому случайному событию А из поля событий F поставлено в соответствие неотрицательное число Р(А), называемое вероятностью события А.

2. Вероятность достоверного события равняется 1 (единице), а вероятность невозможного события равняется 0 (нулю).

3. Вероятность события А определяется в промежутке: 0  Р(А)  1.

4. Если события А₁, А₂, ..., А_n попарно несовместны, то вероятность суммы этих событий равна сумме вероятностей этих событий:

Р(А₁, А₂, ..., А_n) = Р(А₁) + Р(А₂) +...+ Р(А_n)

5. Если события А₁, А₂, ..., А_n представляют полную группу попарно несовместных событий, то вероятность суммы этих событий равна 1, то есть:

Из этой аксиомы следует:

Р(А) + Р(А) = 1 Р(А) = 1 – Р(А)

3билет

"О" Произведением двух событий А и В называется событие АВ, состоящее в том, что произойдёт и событие А, и событие В.

При рассмотрении вопроса произведения двух событий важным понятием является условная вероятность события.

"О" Вероятность события В называется условной, если она вычислена при условии, что событие А произошло, обозначается: Р(В/А).

"Т" Вероятность произведения двух событий равна произведению безусловной вероятности одного из событий на условную вероятность второго события, то есть вычисленную при условии, что первое событие произошло:

Р(АВ) = Р(А)Р(В/А) = Р(В)Р(А/В)

Доказательство: Докажем эту теорему по схеме равновозможных исходов. Пусть результат опыта сводится к появлению одного из n равнозначных исходов.

Пусть некоторому событию А благоприятствует m исходов, а событию В – k исходов, обоим событиям благоприятствует l исходов. Так как все исходы равновозможны, то событие АВ по классической схеме равно отношению l к n, то есть: (1)

Безусловная вероятность события А: (2)

Если произошло событие А, то вероятность того, что произойдёт один из l исходов, то есть что произойдёт событие В, будет равняться: (3)

Очевидно, что выражение (1) равно произведению выражений (2) и (3), то есть: что и требовалось доказать.Теорему о вероятности произведения двух событий можно распространить на вероятность произведения числа событий:

Если события А₁, А₂, ..., А_n независимы, то вероятность произведения этих событий равна произведению их вероятностей:

Теорема о вероятности суммы событий

"О" Суммой двух событий называется событие, заключающееся в том, что произойдёт либо событие А, либо событие В, либо вместе А и В (обозначается: А + В).

"Т" Вероятность суммы двух событий равна сумме их вероятностей минус их произведение: (1)

Доказательство: Согласно определению суммы двух событий можно записать (2)

События, стоящие в правой части данного выражения, являются несовместными, поэтому на основании аксиомы теории вероятностей о сумме несовместных событий можно записать:

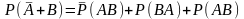(3)

Определим произведение каждого их двух событий правой части:

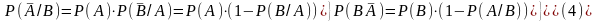
Если подставить выражение (4) в выражение (3) и привести подобные, то получим:

,

, что и требовалось доказать.

Если события и несовместны, то вероятность суммы этих событий равна сумме их вероятностей:

Теорему о вероятности двух событий можно распространить и на вероятность суммы произвольного числа событий:

где – число суммируемых событий.