
- •20. Центральная предельная теорема
- •42.Проверка гипотеза о зависимости (независимости) случайных величин
- •41. Проверка гипотеза о зависимости (независимости) случайных величин
- •2.Билет
- •4Билет Формула полной вероятности
- •7Законы распределения дискретных случайных величин
- •8Распределение непрерывных случайных величин
- •9Системы случайных величин
- •10Условные законы распределения случайных величин, входящих в систему
- •12Нормальный закон на плоскости. Уравнение линии регрессии
- •13Функции от случайных аргументов
- •14 Билет
- •15Закон распределения функции от случайного аргумента общего вида
- •16Законы распределения функции от произвольного числа случайных аргументов
- •17Предельные теоремы теории вероятностей
- •18Частная теорема Чебышева
- •19Теорема Бернулли и Пуассона
20. Центральная предельная теорема
Все рассмотренные формы предельных теорем утверждают одно: сходимость по вероятности тех или иных случайных величин (математического ожидания, вероятности появления события) к определённым постоянным.
Ни в одной из этих теорем не рассматривается вид закона распределения различных композиций случайных величин.
Предельные законы распределения составляют предмет другой группы предельных теорем.
Все формы этих теорем посвящены обоснованию условий, при которых возникает нормальный закон распределения. Так как эти условия часто выполняются на практике, то нормальный закон распределения является наиболее часто встречающимся законом распределения случайной величины.
"Т"
Если случайные величины
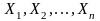 имеют одинаковые
законы распределения с равными друг
другу математическими ожиданиями
имеют одинаковые
законы распределения с равными друг
другу математическими ожиданиями
 и равными дисперсиями
и равными дисперсиями
 ,
то их сумма
,
то их сумма
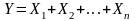 при неограниченном увеличении числа
суммируемых случайных величин стремится
(сходится) к нормальному закону
распределения, соответственно, с
характеристиками:
при неограниченном увеличении числа
суммируемых случайных величин стремится
(сходится) к нормальному закону
распределения, соответственно, с
характеристиками:


На практике если суммируется порядка 5 и более случайных величин, удовлетворяющих условию теоремы, то их сумма приближённо имеет нормальное распределение.
Существует ряд других предельных теорем, связанных с обоснованием того, что сумма случайных величин, имеющих различное распределение, но характеристики которых имеют один и тот же порядок при неограниченном числе суммируемых случайных величин, (эта сумма) также стремится к нормальному закону распределения.
На основании центральной предельной теоремы сформулированы частная и интегральная теоремы Муавра-Лапласа.
Частная теорема:
"Т"
Если проводится
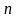 независимых испытаний, в каждом из
которых событие появляется с вероятностью
Р
и число испытаний неограниченно
увеличивается, то биномиальное
распределение может быть заменено
нормальным (апексимировано), то есть:
независимых испытаний, в каждом из
которых событие появляется с вероятностью
Р
и число испытаний неограниченно
увеличивается, то биномиальное
распределение может быть заменено
нормальным (апексимировано), то есть:
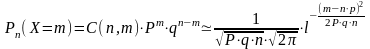
42.Проверка гипотеза о зависимости (независимости) случайных величин
Т.к. степень силы связи между случайными величинами, входящими в систему, определяется коэффициентом кореляции, то при определении независимости случайными величинами, входящими в систему, формируется гипотеза вида:
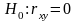
 Где
Где
 - коэффициент кореляции между случайными
величинами X
или Y.
- коэффициент кореляции между случайными
величинами X
или Y.
В качестве выборочной
функции при проверке этой гипотезы
задаётся выражение вида:
 Где
Где
 - статистический коэффициент кореляции.
- статистический коэффициент кореляции.
При справедливости
нулевой гипотезы данная выборочная
функция имеет
 распределение
с числом степеней свободы
распределение
с числом степеней свободы
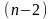 ,
поэтому нулевая гипотеза проверяется
по таблицам
распределения.
,
поэтому нулевая гипотеза проверяется
по таблицам
распределения.
Если не подтверждается гипотеза о независимости случайных величин, то может быть сформулирована гипотеза о силе связи между случайными величинами, входящими в систему:

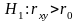
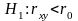
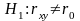
Данная гипотеза проверяется по выборочной функции вида:
 (1)где
- статистический коэффициент корреляции.
(1)где
- статистический коэффициент корреляции.
Если справедлива нулевая гипотеза, то данная выборочная функция имеет стандартное нормальное распределение с характеристиками:
 (2)
(2)
 (3)
(3)
Чтобы нулевую гипотезу можно было проверить по таблицам нормального стандартного распределения, переходят к нормированным и центрированным выборочным функциям:
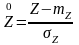 (4)
(4)
Она имеет нормальное стандартное распределение. Поэтому нулевую гипотезу проверяют с помощью таблиц стандартного нормального распределения, т.е. по уровню значимости и виду альтернативной гипотезы определяют критическую область, а по выборочной функции (4) определяют её реализацию.
Если полученный результат попадает в критическую область, то нулевая гипотеза отклоняется.
