Определение тройного интеграла и его основные свойства
ОПРЕДЕЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА |
||
Тройным интегралом от функции f(x, y, z) по области V называется конечный предел трехмерной интегральной суммы при стремлении к нулю ранга разбиения, порождающего эту сумму (если этот предел существует и не зависит ни от способа разбиения области V на элементарные части, ни от выбора точек на каждой из этих элементарных частей):
здесь n – это количество элементарных частей разбиения области V; Pi (xi,yi,zi) – произвольно выбранная точка на каждой элементарной части, i = 1,...,n;
|
—
ранг
разбиения;
– диаметр i-ой
элементарной части.Достаточное условие существования тройного интеграла
Если
функция f (x,y,z)
непрерывная в замкнутой области V,
то 
существует.
Механическая трактовка тройного интеграла
Если f (x,y,z) 0
— это объемная плотность распределения
вещества в области V,
то 
—
это масса всего вещества в трехмерной
области V.
Основные свойства тройного интеграла
Аналогичны
свойствам определенного интеграла по
отрезку 
и
двойного интеграла по области D.
Свойство 1 (линейность тройного интеграла по подынтегральной функции)
,
где 
—
постоянные множители по x, y, z.
Свойство 2 (аддитивность тройного интеграла по области интегрирования)
Если V = V1 V2,
то 
.
Свойство 3 (о значении тройного интеграла от функции, тождественно равной единице)
Если
подынтегральная функция f(x,y,z) 1
для 
,
то тройной интеграл от неё по области V равен
объему (мере) области интегрирования:
(здесь область V и её объём V обозначены одной буквой).
Свойство 4 (оценки значения тройного интеграла)
Если m и M — наименьшее и наибольшее значения функции f(x,y,z) в замкнутой области V, то
Если
|f(x,y,z)|
при (x,y,z)V,
то
Свойство 5 (теорема о среднем значении подынтегральной функции)
Если функция f (x,y,z) непрерывна в области V, то существует хотя бы одна точка P0(x0;y0;z0)V такая, что
При этом
число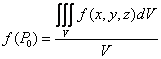 
называется средним
значением
функции f(x,y,z) по области V.