18.Законы распределения вероятностей случайных погрешностей

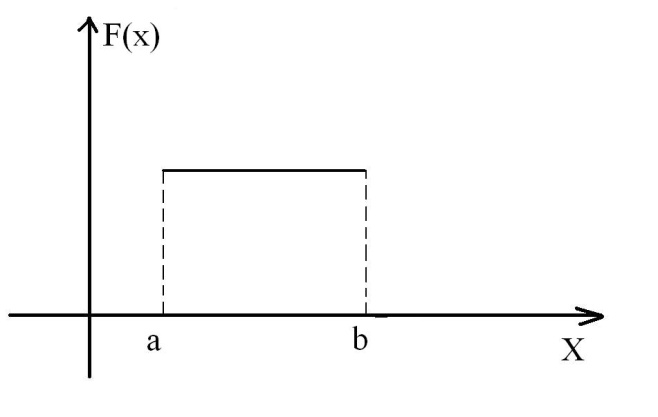1 )Равномерный закон распределения. Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [a, b], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.е.

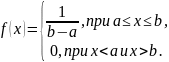
Обозначение: .

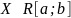Математическое ожидание: .

Дисперсия: .

Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, при статистическом моделировании наблюдений, подчиненных заданному распределению.

2)Нормальный закон распределения. Непрерывная случайная величина X имеет нормальный закон распределения с параметрами a и 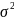, если ее плотность вероятности имеет вид:

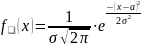
Обозначение: .

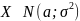Математическое ожидание: .

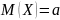Дисперсия: .

Нормальный закон распределения с параметрами 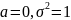, т.е. N(0;1), называется стандартным или нормированным.

Функция распределения нормально распределенной случайной величины имеет вид:

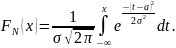
Нормальный закон распределения занимает центральное место в теории и практике вероятностно-статистических методов. Он является предельным законом, к которому приближаются многие другие законы распределения. Центральная предельная теорема теории вероятностей утверждает, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному.

3)Распределение Стьюдента (t-распределение). Пусть – независимые стандартные нормальные случайные величины, такие что . Тогда распределение случайной величины t:

называется распределением Стьюдента с k степенями свободы, .

Обозначение: .

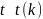Математическое ожидание: .

Дисперсия: .

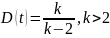Распределение Стьюдента сходится к стандартному нормальному при . Распределение Стьюдента применяется в статистике для построения доверительных интервалов и тестирования гипотез, касающихся неизвестного среднего статистической выборки из нормального распределения.

19.Точечные оценки истинного значения на основании ограниченного ряда наблюдений.

Оценка параметра называется точечной, если она выражается одним числом. Любая точечная оценка, вычисленная на основании опытных данных, является их функцией и поэтому сама должна представлять собой случайную величину с распределением,

Действительное значение измеряемой величины: А, ее оценка: (функция, зависящая от вида распределения измеряемой величины и результата измерения).

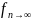= (x₁,x₂..,x_n). Вид таких функций должен удовлетворять некоторым условиям, при которых имеет смысл принимать за наименьшее приближенное значение искомой величины А только оценку .

К точечным оценкам предъявляется ряд требований, определяющих их пригодность для описания самих параметров.

1.Оценка называется состоятельной, если при увеличении числа наблюдений она приближается (сходится по вероятности) к значению оцениваемого параметра.

2.Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру.

3.Оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра.

На практике не всегда удается удовлетворить одновременно все эти требования, однако выбору оценки должен предшествовать ее критический анализ со всех перечисленных выше точек зрения.

Рассмотрим случайную величину х, имеющую функцию распределения F(x). Пусть x₁,x₂..,x_n-выборка, состоящая из n наблюдений величины х. Их можно рассматривать как n независимых величин с одинаковым законом распределения, совпадающим с распределением F(x).

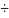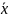M[x_i]=M[x]; Д[x_i]=Д[x]; где i=1 n. В качестве оценки истинного значения применяется среднее арифметическое значение = = . Среднее арифметическое представляет собой лишь оценку математического ожидания результата измерений и может стать оценкой истинного значения измеряемой величины лишь после исключения систематической погрешности. Дисперсия ср арифметического значения в n раз меньше дисперсии единичного наблюдения Д_n[x]= .

=

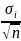
Существует несколько методов определения оценок. Наиболее распространен метод максимального правдоподобия, теоретически обоснованный математиком Р. Фишером. Также используется метод наименьших квадратов. В соответствии с этим методом среди некоторого класса оценок выбирают ту, которая обладает наименьшей дисперсией, т. е. наиболее эффективную оценку. Для случая нормально распределенных случайных погреш­ностей оценки, получаемые методом наименьших квадратов, сов­падают с оценками максимального правдоподобия.

Точечная оценка погрешности измерения-неполная, т.к.указывает на границы интервала, в котором может находиться истинное значение А, но ничего не говориться о вероятности попадания величины А в этот интервал. Точечная оценка позволяет сделать некотрые выводы о точности произведенных измерений, поэтому ее рекомендуется использовать совместно с др результатами измерений, но не как окончательный результат.