Оглавление

1. Алгоритм и его характеристики 2

2. Вычислимые функции и их графики 3

3.Разрешимые и перечислимые множества. Критерий разрешимости множества 4

4.Рекурсивные функции и операторы. Примеры 6

5. Машина Тьюринга и её программа. Машина Тьюринга как алгоритм 9

6. Эффективная нумерация машин Тьюринга 12

7. Неразрешимые алгоритмические проблемы 13

8. Детерминированные конечные автоматы и их работа. Диаграмма и функция переходов. Расширенная функция переходов. Язык ДКА 14

9. Недетерминированные конечные автоматы и их работа. Диаграмма и отношение переходов. Язык НКА 16

10. Недетерминированные конечные автоматы с ε-переходами и их работа. Язык ε-НКА 19

11. Языки. Операции над языками 21

12. Регулярные выражения и их свойства. Язык регулярного выражения 22

13. Регулярные выражения и ДКА 23

14. Свойства регулярных языков. Лемма о накачке. Замкнутость регулярных языков 24

15. Контекстно-свободные грамматики, порождения цепочек, язык грамматики 26

16. Замкнутость и разрешимость КС-языков 28

17. Полезные, порождающие и достижимые символы КС – грамматики. Нормальная форма Хомского КС-грамматики 29

18. Приведение КС-грамматики (контекстно-свободной) к НФХ - грамматике (нормальной форме Хомского) 30

19. Автоматы с магазинной памятью и их работа. Конфигурация МП-автомата и его язык, вычисление. 31

МП-автомат – один из способов задания КС - грамматики 31

20. МП-автоматы (с магазинной памятью) и КС-грамматики 33

21. Эффективная нумерация машин Тьюринга. Язык диагонализации и универсальный язык. 35

Эффективная нумерация машин Тьюринга 35

22. Рекурсивный и рекурсивно-перечислимые языки. Иерархия языков по Хомскому 37

23. Временная сложность машин Тьюринга. Классы P и NP языков и связь между ними 38

24. NP – полные проблемы 39

1. Алгоритм и его характеристики

Алгоритм – точная система инструкций о выполнении в определенном порядке некоторых действий для решения всех задач некоторого класса. (Это интуитивное понятие).

Каждый алгоритм характеризуется следующими 5 свойствами:

1. Дискретность алгоритма – процесс получения некоторых величин идущий в дискретном времени так, что в начальный момент задается некоторая начальная система величин, а в каждый следующий момент система величин получается по определенному закону (программе) из системы величин, полученных в предыдущий момент.

2. Детерминированность - система величин, полученных в какой-то неначальный момент. Однозначно определяется системой величин, полученных в предыдущий момент.

3. Элементарность шагов. Закон получения последующей системы величин должен быть простым и локальным.

4. Направленность алгоритма. Если способ получения последующих систем величин из какой-то заданной не дает результата, то должно быть указано, что считать результатом.

5. Массовость. Начальные данные (начальная система величин) должны выбираться из потенциального бесконечного множества.

Примеры: действия арифметики.

«Алгоритм» раньше писалось как «алгорифм» (Мухамед ал Харизми)

Примеры:

1. 2/0 = 99…9… – не натуральное число.

2. a:0 = х

а) а = х∙0 = 0 =>?! (если а≠0)

б) 0 :0 = х

0 = 0∙х => частное любое

2. Вычислимые функции и их графики

В теории рассматриваются n-местные функции:

;

, т. е. рассматриваются целочисленные функции целочисленного аргумента.

Опр. Функция называется вычислимой, если существует алгоритм, позволяющий вычислить значение этой функции для тех наборов переменных, на которых она определена и работающая вечно на тех наборах, на которых она не определена.

Опр.: Если область определения 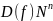(собственное подмножество ) и функция вычислима, тогда она называется частично вычислимой.

Пример: , - частично вычислимая.

Опр.: Класс вычислимых функций, удовлетворяющий 5-ти свойствам алгоритма строится однозначно и называется классом рекурсивных функций.

3 типа функций:

- функция следования;

- тождественный ноль;

- функция-проектор.

x – проекция для (х; у) на ось Ох.

Опр.: График вычислимой функции – это множество картежей вида

В зависимости от графика классифицируются сами функции.

3.Разрешимые и перечислимые множества. Критерий разрешимости множества

Опр. Множество M называется разрешимым, если имеется алгоритм для выяснения того, принадлежит ли данный кортеж этому множеству, или нет.

С каждым множеством можно связать функцию

(характеристическая функция)

Теорема 1. Множество М разрешимо тогда и только тогда, когда его характеристическая функция вычислима.

Опр. . Множество М (рекурсивно, эффективно алгоритмически) перечислимо, если оно либо пусто, либо является областью значений некоторой вычислимой функции.

Теорема 2. Даны 2 множества M и K. Если оба этих множества перечислимы, то перечислимы и их объединения, и их пересечения.

Пусть f – алгоритм, который перечисляет М: ,

Пусть g – алгоритм, который перечисляет K: .

Надо доказать, что .

Док-во:

Построим алгоритм, который перечисляет . Породим элементы

Породим

Теорема 3. Множество М разрешимо  оно само М и его дополнение перечислимые. (Критерий разрешимости множества).

Доказательство:

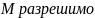. Оно не пусто. Если хотя бы один элемент , то - вычислима. Надо доказать, что перечислимы.

Для этого надо построить алгоритм, который порождает элементы М и

.

перечисляет элементы множества М, она построена по характеристической функции, которая вычислима; значит, функция f вычислима, М – множество значений вычислимой функции, по определению М – перечислима.

Теперь для . ;

g – вычислима, поэтому  – перечислимо.

M, – перечислимы => М – множество значений вычислимой функции.

; - область знач. пер. ф-ции.

f, g - вычислимы. Строим алгоритм. , позволяющий выяснить принадлежит ли данное натуральное число М или не.

Порождаем первые элементы и сравниваем

.

Последовательно порождаем пары и сравниваем n = f(0) или n = g(0). В итоге n = f(i) или n = g(j). Т.к. есть алгоритм перечисления, то множество М – разрешимо. Ч.т.д.

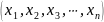- эти кортежи можно пронумеровать, существует диагональный метод нумерации кортежей, либо канторовская нумерация.

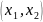- кортеж длины 2. Неважно какие значения принимают , нумеруются номера пар.

- диагональная нумерация.

Возьмёт пару . Какой номер она имеет?

.

– четверки

.

Все кортежи длины n можно пронумеровать.

Теорема 4:Существует перечислимое, но не разрешимое множество

Множество перечислимо, если существует функция его порождающая, например, - перечислимое. . Это разрешимое множество, т.к. для любого числа можно определить является ли оно кубом.

Доказательство:

Построим множество, которое будет перечислимым, но не разрешимым.

(идея доказательства).

эффективное перечисление всех перечислимых множеств, по номеру множества можно восстановить множество.

Построим алгоритм порождающий множество U.

На шаге с номером С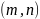 этот алгоритм вычисляет (порождает) m-ный элемент множества .

Если оказывается, что этот элемент совпадает с n , то алгоритм относит его к U, т.е. .

Это множество U – перечислимо (по построению).

Его дополнение , т.е. состоит из элементов . Это значит, что множество отличается от хотя бы одним элементом. Это дополнение нельзя перечислить, оно не разрешимо (по Теореме 3).