
- •1.Частн.Прирощ., произв., диф., их геом.Смысл.
- •2. Полный диф.Ф-ции нескольких переменных. Инвариантность ф-ции полн.Диф.
- •3. Необход. И дост. Условие диф. Ф-ции
- •6. Экстремум ф-ции нескол. Переем. Необх. И дост. Усл.
- •8. Первообр. Ф-ции и неопред. Инт.
- •12. Инт. Рациональных дробей
- •14. Инт. Тригонометрических выражений
- •15. Инт. Некот иррациональных выражений
- •16. Определенный инт. Геометр.Смысл
- •4. Произв.Сложных и неявнозад.Ф-ций
- •5. Кас.Пл. И норм. К поверхн. Скал.Поле. Градиент
- •7. Условный экстр. Метод множит. Лагранжа
- •11. Замена переменной в неопред. Инт.
- •13. Инт. Простейших рациональных ф-ций
- •17. Основные св-ва опред. Инт.
- •18. Формула Ньютана-Лейбница
- •19. Опред.Инт. С переменным верхним пределом
1.Частн.Прирощ., произв., диф., их геом.Смысл.
Пусть
ф-ция
 определена в некот.
определена в некот.
 - окр.
точки
- окр.
точки
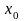 и
и
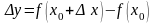 – ее приращение в этой точке,
соответствующее приращению аргумента
– ее приращение в этой точке,
соответствующее приращению аргумента
 ,
где
,
где
 .
.
Предел
отношения
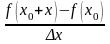 при
при
 при условии, что последнее произвольным
образом стремится к нулю наз. част.
производной
ф-ции
в точке
.
Геометрический смысл производной
состоит в том, что произв. ф-ции
при данном значении
аргумента равна угловому коэффициенту
касательной к графику этой ф-ции в точке
при условии, что последнее произвольным
образом стремится к нулю наз. част.
производной
ф-ции
в точке
.
Геометрический смысл производной
состоит в том, что произв. ф-ции
при данном значении
аргумента равна угловому коэффициенту
касательной к графику этой ф-ции в точке
 ,
т. е.
,
т. е.
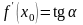 ,
где
,
где
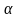 – величина угла, образованного
касательной с положительным направлением
оси
– величина угла, образованного
касательной с положительным направлением
оси
 ,
поэтому уравнение касательной к графику
ф-ции
в точке
,
поэтому уравнение касательной к графику
ф-ции
в точке
 ,
где
,
где
 ,
имеет вид:
,
имеет вид:
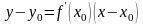 .
Прямая, проходящая через точку
,
перпендикулярно к касательной, наз.
нормалью к
графику ф-ции
в этой точке.
Если
.
Прямая, проходящая через точку
,
перпендикулярно к касательной, наз.
нормалью к
графику ф-ции
в этой точке.
Если
 ,
нормаль имеет уравнение
,
нормаль имеет уравнение
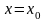 .Операция
нахождения производной ф-ции наз.
дифференцированием
этой ф-ции.
.Операция
нахождения производной ф-ции наз.
дифференцированием
этой ф-ции.
2. Полный диф.Ф-ции нескольких переменных. Инвариантность ф-ции полн.Диф.
Если
ф-ция z=f(x,y)
диф. в т.Р0(х0,у0),
то главная линейная относительно
прирощения аргумента часть ее полн.
приращения наз. диф. ф-ции: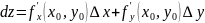
П![]() риращения
риращения
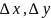 наз. диф.независимых переменных, кот.
Равны dx,
dy:
dz=dxz
+ dyz
.Пусть дана сложная ф-ция y = f(u ), u =u(x)
. Если сущ. произв.
наз. диф.независимых переменных, кот.
Равны dx,
dy:
dz=dxz
+ dyz
.Пусть дана сложная ф-ция y = f(u ), u =u(x)
. Если сущ. произв.
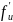 ,
, и , то по правилу диф.ния сложной ф-ии
и , то по правилу диф.ния сложной ф-ии
![]() .
Умножим обе части этого равенства на
dx, получим
.
Умножим обе части этого равенства на
dx, получим
![]()
Но![]() ,
тогда в случае сложной ф-ции имеем
,
тогда в случае сложной ф-ции имеем
![]() Сравнивая
ф-лы (6.4) и (6.5), видим, что они совпадают
по форме записи. Однако эти ф-лы имеют
различный смысл: в первой из них dx =
∆x , а во второй du = u′(x)dx . Таким обр.,
диф. ф-ции всегда равен произведению
произв. на диф. аргумента и не зависит
от того, является ли переменная, по
кот. взята произв., ф-цией или
незав.переменной. В этом заключается
св-во инвариантности (неизменности)
формы
Сравнивая
ф-лы (6.4) и (6.5), видим, что они совпадают
по форме записи. Однако эти ф-лы имеют
различный смысл: в первой из них dx =
∆x , а во второй du = u′(x)dx . Таким обр.,
диф. ф-ции всегда равен произведению
произв. на диф. аргумента и не зависит
от того, является ли переменная, по
кот. взята произв., ф-цией или
незав.переменной. В этом заключается
св-во инвариантности (неизменности)
формы
диф.
И полный диф.
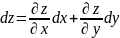 .
.
3. Необход. И дост. Условие диф. Ф-ции
Ф-ция
z=f(x,y)
наз. диф. в
т.Р0(х0,у0),
если ее полное приращение в этой точке
можно представить в виде

Где
А,В – постоянные, завяс.от х,у;
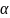 ,
,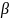 - бмф, причем их пределы=0. Т.: если ф-ция
диф. в точке, то она и непрерывна в этой
т. Т.1(необх.): если ф-ция диф. в т., то она
имеет в этой т. частные производные.
Т.2.(дост.): если ф-ция имеет частные
произв. в т., непрерывная в самой этой
т., то то она диф. в этой т. Р0(х0,у0).
- бмф, причем их пределы=0. Т.: если ф-ция
диф. в точке, то она и непрерывна в этой
т. Т.1(необх.): если ф-ция диф. в т., то она
имеет в этой т. частные производные.
Т.2.(дост.): если ф-ция имеет частные
произв. в т., непрерывная в самой этой
т., то то она диф. в этой т. Р0(х0,у0).
6. Экстремум ф-ции нескол. Переем. Необх. И дост. Усл.
Точки
макс. или мин. ф-ции наз. точками
экстр-а ф-ции,
а максимумы и минимума наз. экстр-ами
ф-ции. Экстр. ф-ции носят локальный х-р
– это наиб. или наим. знач. ф-ции по
сравнению с близлежащими ее знач. Наиб.
или наим. значения ф-ции
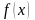 в обл. ее определения или на отр.
в обл. ее определения или на отр.
 в отличие от локальных ее экстр. наз.
соответственно абсолютными
(или глобальными)
максимумом
и минимумом
и обозн.
в отличие от локальных ее экстр. наз.
соответственно абсолютными
(или глобальными)
максимумом
и минимумом
и обозн.
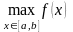 ,
,
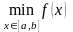 .
Необх. условие экстр. ф-ции выражается
т-мой Ферма. Если дифференцируемая в т
ф-ция
имеет в этой т локальный экстр., то ее
произв.
.
Необх. условие экстр. ф-ции выражается
т-мой Ферма. Если дифференцируемая в т
ф-ция
имеет в этой т локальный экстр., то ее
произв.
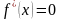 .
Т-ма имеет простой геом. смысл: кас. к
графику диф. ф-ции в точке экстр.
параллельна оси
.
Т-ма имеет простой геом. смысл: кас. к
графику диф. ф-ции в точке экстр.
параллельна оси
 .
Точки, в кот.
,
наз. стационарными.
Т., в кот ф-ция непрерывна, а ее произв.
равна 0 или обращается в
.
Точки, в кот.
,
наз. стационарными.
Т., в кот ф-ция непрерывна, а ее произв.
равна 0 или обращается в
 ,
или не сущ., наз. критическими
точками или
точками
возможного экстремума ф-ции.
Крит. точка
наз. угловой
точкой ф-ции
,
если сущ.
,
или не сущ., наз. критическими
точками или
точками
возможного экстремума ф-ции.
Крит. точка
наз. угловой
точкой ф-ции
,
если сущ.
 и т возврата ф-ции, если ее левая
и т возврата ф-ции, если ее левая
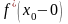 и правая
и правая
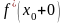 произв. бескон. (касс. к графику
в точке
парал. оси
произв. бескон. (касс. к графику
в точке
парал. оси
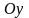 ).
Достат. услов. экстр. Пусть в стацион.
т (x0, y0) и некот. ее окрестн. ф-ция f ( x, y)
имеет непрерывные частные проив.
второго порядка включительно. Вычислим
в точке (x0 , y0) значения
).
Достат. услов. экстр. Пусть в стацион.
т (x0, y0) и некот. ее окрестн. ф-ция f ( x, y)
имеет непрерывные частные проив.
второго порядка включительно. Вычислим
в точке (x0 , y0) значения
![]() Тогда: 1) если ∆ >
0, то ф-ия f ( x, y) в т имеет экстр.;макс.,
если A<0; мин., если A > 0
Тогда: 1) если ∆ >
0, то ф-ия f ( x, y) в т имеет экстр.;макс.,
если A<0; мин., если A > 0
2) если ∆ < 0, то ф-ция f ( x, y) в т (x0, y0) экстр. не имеет; 3) если ∆=0, то экстр. в т может быть, может не быть. Необходимы дополн. исслед.
