9.Баланс мощности. Мощность потерь и кпд. Режимы работы электрической цепи постоянного тока.

Согласно закону Джоуля-Ленца, вся электрическая энергия, сообщаемая проводнику в результате работы сил электрического поля, превращается в тепловую энергию:

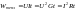[Дж]

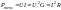[Вт]

По обобщенному закону Ома.

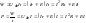
Выражения, записанные для ветви с источником напряжения, справедливы и для ветви с источником тока, если произвести подстановку 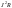вместо 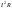и вместо .

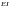Отсюда следует закон сохранения энергии, согласно которому алгебраическая сумма мощностей, подводимых ко всем ветвям разветвленной электрической цепи, равна нулю:

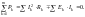
Существует еще одна форма записи баланса мощности:

.

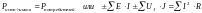В левой части суммируются мощности источников энергии, а в правой – мощности, преобразованные в потребителях в тепло. Мощности источников, отдающих энергию, берутся со знаком «+», а работающих в режиме потребителей – со знаком «–».

В соответствии с законом сохранения энергии очевидно следующее утверждение для электрической цепи: "В электрической цепи, содержащей несколько источников электрической энергии и несколько диссипативных элементов, суммарная мощность, выделяемая источниками электрической энергии, равна суммарной мощности, рассеиваемой (потребляемой) диссипативными элементами". Это положение называется условием баланса мощностей.

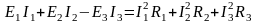В общем случае условие баланса мощностей можно представить следующим соотношением:

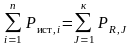. (1.7)

или

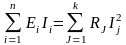
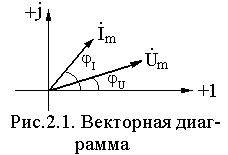, (1.8)

где n – число источников ЭДС, к – число диссипативных элементов.

Точность расчета оценивается с помощью относительной погрешности в процентах по формуле:

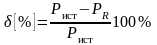, (1.9)

где P_ист – суммарная мощность всех источников цепи, P_R – суммарная мощность, потребляемая всеми диссипативными элементами

10) Преобразования ветвей с источниками эдс. Взаимные преобразования звезды и треугольника сопротивлений.

11) Метод преобразования электрической цепи. Метод непосредственного применения законов Кирхгофа.

12) Метод контурных токов.

При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего определяют токи ветвей через контурные токи.

У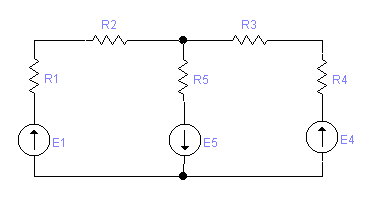 равнения составляют относительно контурных токов, после чего определяют токи ветвей через контурные токи.

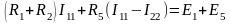
или

Для второго контура

или

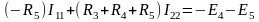
Введем обозначения

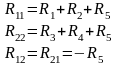
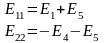
С учетом введенных обозначений

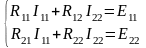
где

.

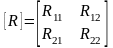
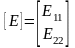Получим представление в матричном виде

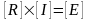
Общее решение системы n – уравнений относительно тока.

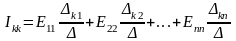, где ∆ - определитель системы.

;

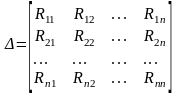∆_km – алгебраическое дополнение полученное из определителя ∆ путем вычеркивания k-столбца и m-й строки и умножения полученного определителя на (-1)^k+m.

Пример.

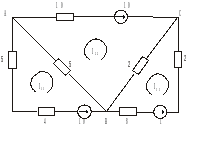
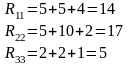
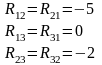
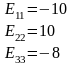
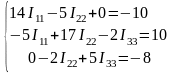
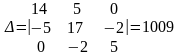
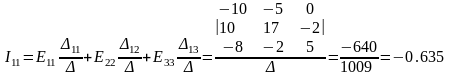
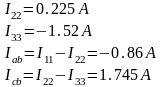
13)Метод узловых потенциалов

Ток в любой ветви схемы можно найти по закону Ома для участка цепи, содержащего Э.Д.С. Для того чтобы можно было применить закон Ома, необходимо знать потенциалы узлов схемы. Метод расчета электрических цепей, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов.

Допустим, что в схеме n – узлов. Так как любая точка схемы может быть заземлена, то можно принять потенциал его равным нулю. При этом число неизвестных уменьшается с n до n – 1.

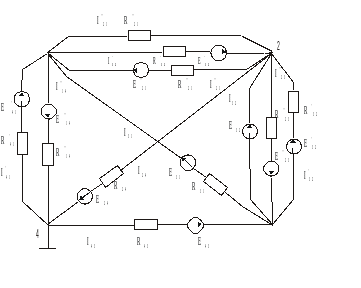Узел 4 заземлен, те. ₄= 0. Необходимо определить ₁,₂,₃ - ?

Первый индекс – номер узла, от которого ток утекает, второй индекс – номер узла к которому ток подтекает. Составим уравнение по первому закону Кирхгофа для первого узла:

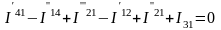
Перепишем последнее уравнение следующим образом

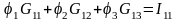
где

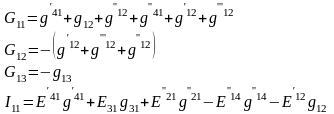
Множителем при ₁ является коэффициент G₁₁, равный сумме проводимостей всех ветвей, сходящихся в первом узле. G₁₂ равняется сумме проводимостей всех ветвей, соединяющих узел 1 с узлом 2, взятой со знаком минус. G₁₂ есть сумма проводимостей всех ветвей, соединяющих узел 1 с узлом 3, взятая со знаком минус. Ток I₁₁, называемый узловым током первого узла, - это расчетная величина, равная алгебраической сумме токов, полученной от деления Э.Д.С. ветвей, подходящих к узлу 1, на сопротивление данных ветвей. В эту сумму со знаком плюс входят токи тех ветвей, Э.Д.С. которых направлены к узлу 1.