12. Неоднородные лду. Метод вариации произвольных постоянных

Рассмотрим линейное неоднородное дифференциальное уравнение n-го порядка

, (1)

где , …, , - непрерывные функции, в том числе постоянные.

Теорема (о структуре общего решения неоднородного линейного уравнения). Общее решение (1) - это сумма общего решения однородного уравнения

, (2)

и любого частного решения неоднородного уравнения (1), т.е.если , ,…, линейно не зависимые решения уравнения (2), то общее решение уравнения (1) имеет вид

,

где , ,…, - произвольные постоянные.

Доказательство. Докажем утверждение только для уравнения:

, (3)

так как в общем случае доказывается аналогично.

Итак, пусть - общее решение соответствующего однородного уравнения

. (4)

Пусть - произвольное частное решение неоднородного уравнения (3). Непосредственной подстановкой в уравнение (3) можно проверить, что при любых значениях постоянных , функция является решением (3).

Пусть заданы начальные условия и . По определению общего решения мы должны доказать, что при определенных значениях постоянных , из получается частное решение, удовлетворяющее заданным начальным условиям.

Заметим, что из линейной независимости решений , следует, что . Поэтому система имеет единственное решение , . Таким образом, является решением уравнения (3), к тому же удовлетворяющим начальным условиям и . 

Теорема (метод вариации постоянных). Частное решение уравнения (1) - это , где - фундаментальная система решений (2), а функции находятся из системы

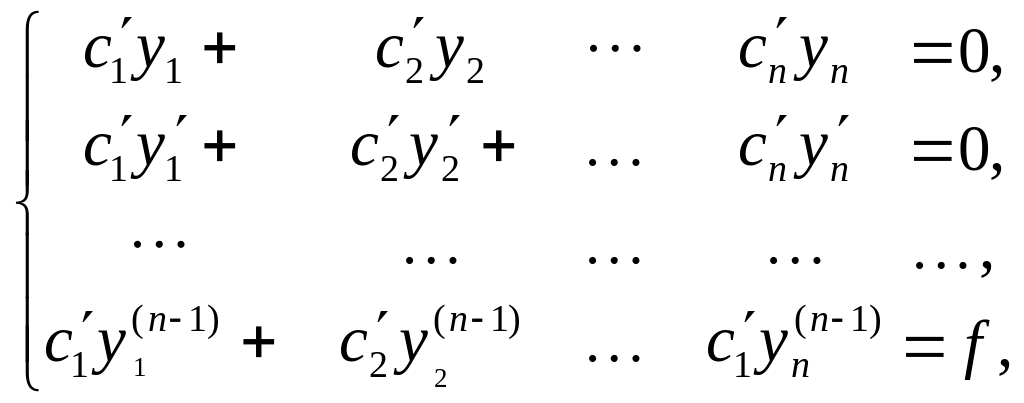(5)

Доказательство. Докажем утверждение только для , т.е. для уравнения (3), так как в общем случае доказывается аналогично.

Итак, пусть - общее решение соответствующего однородного уравнения (4). Рассматривая как функции переменной , найдем .

Мы имеем одно дифференциальное уравнение (3), но две неизвестные функции . Поэтому наложим дополнительное ограничение

. (6)

Учитывая (6) в равенстве для производной, запишем .

Отсюда

.

Подставляя выражения для производных в (3) и учитывая, что - решения (4), получим

. (7)

Объединяя в систему (6), (7), получим (5) для . 

Пример. Найти общее решение уравнения .

Решение. Решение ищем в виде суммы общего решения однородного уравнения и любого частного решения неоднородного уравнения.

Для нахождения запишем характеристическое уравнение , корни которого кратности , , . Отсюда .

Далее применяем метод вариации постоянных:

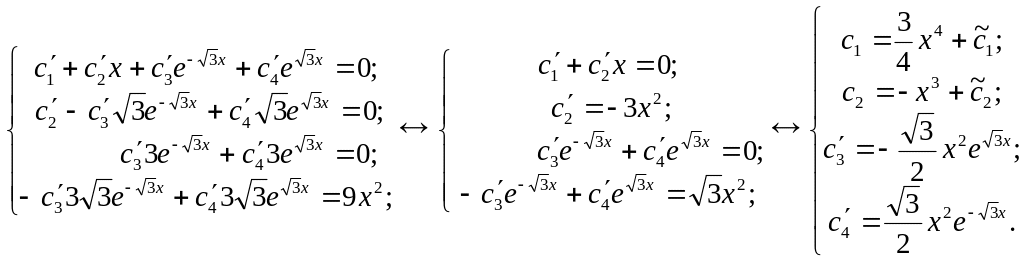Дважды интегрируя по частям, находим:

Общее решение неоднородного уравнения:

После преобразований получим:

Подстановкой в уравнение убеждаемся, что является частным решением неоднородного уравнения.

Ответ:

Найти общее решение:

1. . 2. . 3. . 4. .

5. . 6. . 7. . 8. .