8. Уравнения, не разрешенные относительно , Лагранжа, Клеро, Риккати

1. Для решения уравнения вида 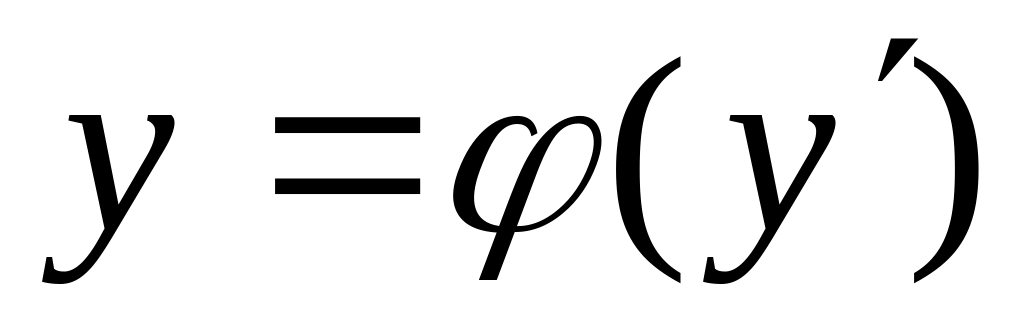, не разрешенного относительно , не содержащего явно независимую переменную , вводим параметр : .

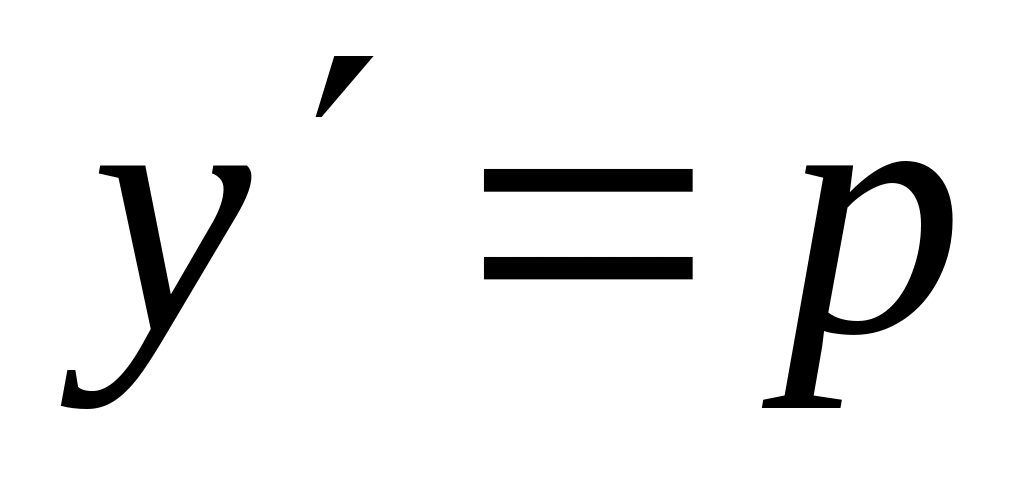Записываем дифференциал , учитывая, что ,

.

Общее решение уравнения: , .

Пример. Найти общее решение .

Решение. Вводим параметр (по условию ) получаем

.

Записываем дифференциал , учитывая, что ,

.

Ответ: Общее решение уравнения: , .

2. Решение уравнения вида , не разрешенного относительно , не содержащего явно , записывается также в параметрической форме: ,

.

Записываем дифференциал , учитывая, что ,

.

Ответ: Общее решение уравнения: , .

Пример. Найти общее решение .

Решение. Вводим параметр , .

Записываем дифференциал , учитывая, что ,

.

Общее решение уравнения: , . 

3. Уравнение вида , где и - заданные функции переменной , называется уравнением Лагранжа. Вводим параметр : .

Записываем дифференциал этой функции, учитывая, что ,

.

Если получим линейное уравнение первого порядка

,

решение которого вместе с дает общее решение.

При делении на могут быть потеряны решения, соответствующие значениям параметра , при которых . Удовлетворяющие этому равенству значения параметра надо подставить в выражение , получив, таким образом, функцию . Если эта функция является решением уравнения Лагранжа, то оно может быть частным решением, если входит в совокупность, определяющую общее решение, или особым, в противном случае.

Пример. Решить уравнение: .

Решение. Уравнение: является уравнением Лагранжа, здесь

, . Вводим параметр , получаем .

Записываем дифференциал этой функции, учитывая, что ,

или получим линейное уравнение первого порядка .

Полагаем .

Выберем с условием, что .

Следовательно,

При из равенства получим решение , являющееся особым решением.

Ответ: Общее решение , ; - особое решение.

4. Уравнение вида , где - заданная функция переменной , называется уравнением Клеро. Уравнение Клеро – частный случай уравнения Лагранжа. Вводя параметр , получаем

.

Записываем дифференциал этой функции, учитывая, что ,

.

Полагая , получаем общее решение уравнения Клеро .

Заметим, что общее решение уравнения Клеро может быть получено формальной заменой .

Из равенства находим особое решение уравнения Клеро, задаваемое в параметрической форме, , .

Пример. Решить уравнение .

Решение. Сначала преобразуем до вида уравнения Клеро . Вводя параметр , получаем

.

Записываем дифференциал этой функции, учитывая, что ,

.

Полагая , получаем общее решение уравнения Клеро .

Из равенства находим особое решение уравнения Клеро, задаваемое в параметрической форме, , или . Исключая параметр , получим .

5. Уравнение вида называется уравнением Риккати [1]. В общем случае это дифференциальное уравнение неразрешимо в квадратурах. Если же известно одно частное решение , то введением нового переменного по формуле уравнение Риккати может быть сведено к линейному дифференциальному уравнению

Пример. Найти общее решение .

Решение. Это уравнение Риккати с , , . Заметим, что, если , то . Поэтому является частным решением. Выполним замену . Получим и или , т.е. . Полагаем . Отсюда . В итоге

.

Находим из уравнения , т.е. и .

Следовательно, и . Отсюда и .

Поэтому общее решение . 

Задачи:

1. Определите типы дифференциальных уравнений, выбрав нужный ответ из данного списка: а) уравнение, не разрешенное относительно производной, не содержащее явно зависимую переменную; б) уравнение, не разрешенное относительно производной, не содержащее явно независимую переменную; в) уравнение Клеро; г) уравнение Лагранжа; д) уравнение Риккати.

1.1. . 1.2. . 1.3. . 1.4. .

1.5. . 1.6. . 1.7. . 1.8. . 1.9. .1.10. . 1.11. . 1.12. .

1.13. . 1.14. .

2. Для совокупностей функций 2.1-2.8 определите тип уравнения из данного списка: а) уравнение, не разрешенное относительно производной, не содержащее явно зависимую переменную; б) уравнение, не разрешенное относительно производной, не содержащее явно независимую переменную; в) уравнение Клеро; г) уравнение Лагранжа, общим решением которого они являются.

2.1. , . 2.2. .

2.3. . 2.4. . 2.5. . 2.6. . 2.7. ; . 2.8. ; .

Разные задачи на уравнения первого порядка:

Найти общий интеграл: 3.1. . 3.2. . 3.3. . 3.4. . 3.5. . 3.6. . 3.7. .3.8. . 3.9. . 3.10. . 3.11. .

3.12. . 3.13. . 3.14. . 3.15. . 3.16. .

3.17. . 3.18. .

Решить задачу Коши:

4.1. , . 4.2. , .

4.3. , . 4.4. , .

4.5. , . 4.6. , .

4.7. , . 4.8. . .

4.9. , . 4.10. , .

4.11. . . 4.12. , .

4.13. . . 4.14. , .

9.ДУ n-го порядка. Теорема Коши. Простейшие случаи понижения порядка

Дифференциальное уравнение n-го порядка имеет вид: ,

или, если его можно разрешить относительно -й производной,

. (1)

Задача Коши для дифференциального уравнения n-го порядка - это система, состоящая из уравнения или (1), и начальных условий:

, ,…, . (2)

Задача Коши состоит в отыскании решения , удовлетворяющего уравнению или (1) и начальным условиям (2).

Пример. Рассмотрим прямолинейное движение точки массы под действием силы , зависящей от , положения точки и ее скорости. По второму закону Ньютона получим дифференциальное уравнение второго порядка: , интегрируя которое получим .

Для получения определенного решения задачи нужно задать еще начальные условия движения, а именно, положение точки ее скорость в начальный момент, т.е. , .

Теорема (Коши для ДУ n-го порядка) [8]. Если в дифференциальном уравнении (1) функция удовлетворяет следующим условиям: непрерывна в некоторой , содержащей точку с координатами , , ,…, и ее производные по переменным также непрерывны в той же области, то существует единственное решение задачи Коши (1), (2).

Замечание. Изменяя в начальных условиях постоянные , ,…, , получим семейство решений, зависящее от произвольных постоянных (общее решение).

Если решение записано в неявном виде , то его называют общим интегралом.

Рассмотрим простейшие случаи понижения порядка дифференциального уравнения.

1. Уравнение вида . Общее решение находится постепенным интегрированием, учитывая, что .

Пример. Найти общее решение дифференциального уравнения .

Решение. Обозначим . Получили уравнение первого порядка с разделяющими переменными. Отсюда . Вновь получили уравнение с разделяющими переменными. Поэтому .

Ответ: .

2. - уравнение, не содержащее в явном виде.

Обозначим . Получим дифференциальное уравнение первого порядка.

Пример. Найти общее решение дифференциального уравнения

.

Решение. Обозначим . Получили линейное уравнение первого порядка. Полагаем

.

Выберем из условия:

.

Далее находим : .

Следовательно, .

В итоге,

.

Ответ: .

3. - уравнение, не содержащее в явном виде.

Обозначим . Получим дифференциальное уравнение первого порядка.

Пример. Найти общее решение дифференциального уравнения .

Решение. Обозначим . Получили уравнение первого порядка с разделяющимися переменными. Отсюда

. Получили вновь уравнение первого порядка с разделяющимися переменными. Поэтому

. 

Найти решения:

1. 1. . 1.2. . 1.3. . 1.4. .

1.5. . 1.6. . 1.7. . 1.8. . 1.9. . 1.10. .

Решить задачу Коши:

11. , , . 12. , , .

13. , , . 14. , , .

Задачи для самостоятельного решения:

2.1. ; 2.2. ; 2.3. ; 2.4. ; 2.5. , , ; 2.6. , , ; 2.7. ; 2.8. , , ; 2.9. ; 2.10. , , .

Ответы: 2.1. ; 2.2. ; 2.3. ; 2.4. ; 2.5. ; 2.6. ; 2.7. ; 2.8. ; 2.9. ; 2.10. .

10. ЛДУ n-го порядка. Определитель Вронского

Линейным дифференциальным уравнения n-го порядка называется уравнение вида , где , …, , - непрерывные функции, заданные на некотором интервале.

Если , то уравнение называется линейным однородным дифференциальным уравнения n-го порядка.

Замечание. Условия теоремы Коши выполнены в силу предположения о непрерывности , …, , .

Теорема (о линейном пространстве решений). Множество решений линейного однородного дифференциального уравнения -го порядка

(1)

образуют линейное пространство, т.е. если и - решения (1), то любая их линейная комбинация является решением (1). Другими словами, множество решений линейного однородного дифференциального уравнения -го порядка замкнуто относительно операции сложения и умножения на число.

Доказательство. Итак, пусть и - решения (1). Рассмотрим произвольную их линейную комбинацию . В силу линейности операции дифференцирования имеем

,

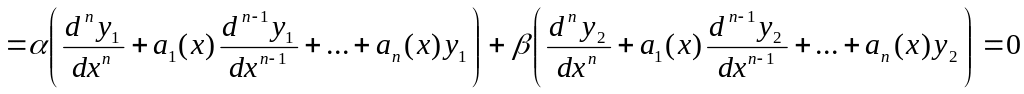т.е. удовлетворяет уравнению (1). 

Функции , ,…, называются линейно независимыми на интервале , если они не связаны никаким тождеством , где - какие-нибудь постоянные, не равные нулю одновременно. В противном случае, функции , ,…, линейно зависимые.

В частности, , линейно независимы на интервале , если и линейно зависимы, если существует постоянная , такая, что .

Рассмотрим определитель Вронского:

, …, .

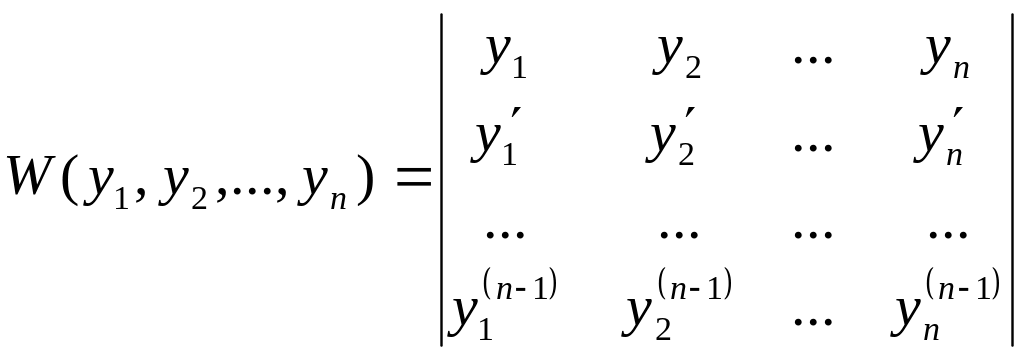Замечание. Из курса алгебры известно, что линейная зависимость столбцов влечет равенство нулю определителя. Поэтому если , ,…, линейно зависимы на интервале , то определитель Вронского тождественно равен нулю в этом интервале .

Теорема (об определителе Вронского). Если , ,…, линейно не зависимые на интервале решения уравнения (1), то определитель Вронского ни в одной точке .

Доказательство. Докажем утверждение только для уравнения

,

так как в общем случае доказывается аналогично.

Пусть вопреки утверждению теоремы существует , такое, что . Заметим, что удовлетворяет уравнению и начальным условиям и . С другой стороны, в силу предположения система 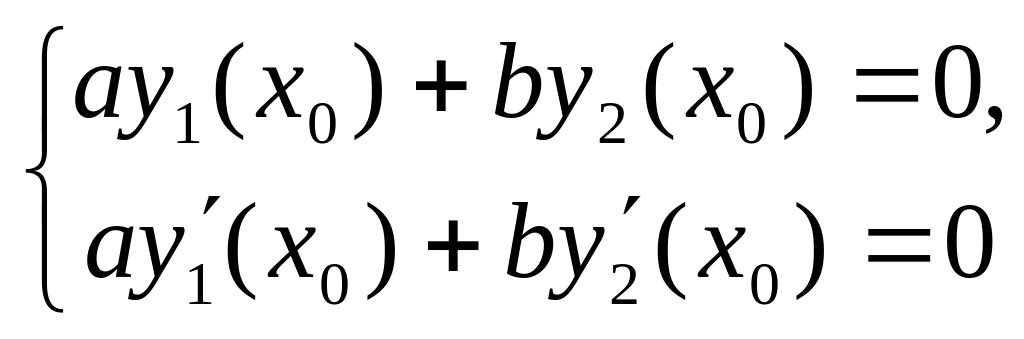имеет ненулевое решение и . Так как множество решений линейного однородного уравнения образует линейное пространство, то является также решением уравнения , к тому же удовлетворяющим начальным условиям и . Полученное противоречие с теоремой Коши о существовании и единственности решения завершает доказательство теоремы. 

Замечание. Базис - мерного линейного пространства всех решений уравнения (1) называется фундаментальной системой решений. Другими словами, максимальное количество линейно независимых решений уравнения (1) равно порядку этого уравнения.

Теорема (о структуре общего решения однородного линейного уравнения). Если , ,…, линейно не зависимые решения уравнения (1), то общее решение уравнения (1) имеет вид , где , ,…, - произвольные постоянные.

Доказательство. Докажем утверждение только для уравнения

,

так как в общем случае доказывается аналогично.

Пусть заданы начальные условия и . По определению общего решения мы должны доказать, что при определенных значениях постоянных , из получается частное решение, удовлетворяющее заданным начальным условиям.

Заметим, что из линейной независимости решений , следует, что . Поэтому система 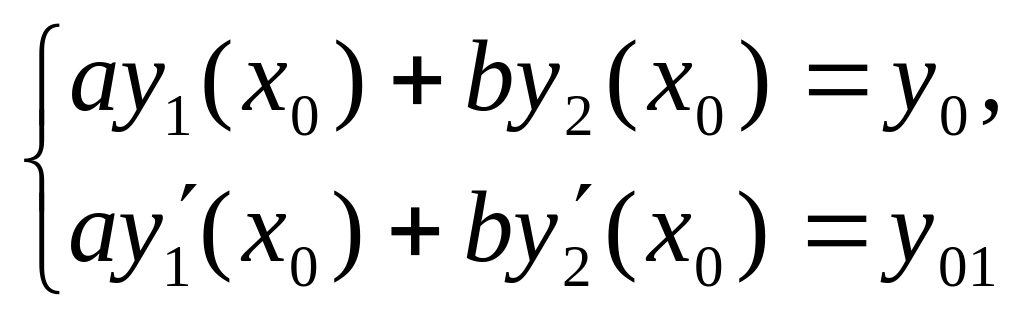имеет единственное решение , . Так как множество решений линейного однородного уравнения образует линейное пространство, то является также решением уравнения , к тому же удовлетворяющим начальным условиям и . 