2. Применение ду для решения физических и геометрических задач
Рассмотрим примеры физических процессов, описываемых простейшими дифференциальными уравнениями.
1. Радиоактивный распад. Известно, что скорость распада любого радиоактивного элемента прямо пропорциональна его точечной массе.
Пусть в момент
времени
масса радиоактивного вещества есть
(в некоторых единицах измерения). В
частности, обозначим через
начальную массу вещества в начальный
момент времени
.
Тогда закон распада можно описать дифференциальным уравнением
,
.
Напомним, что
вещество распадается, т.е. его масса
убывает
со временем, тогда как
(t)
есть «скорость возрастания», т.е.
приращения массы.
Можно проверить
(прямой подстановки), что функция
есть решение нашего уравнения распада
удовлетворяющее начальному условию
,
так что выражения описывает процесс радиоактивного распада.
2. Остывание нагретых тел. Пусть имеется некоторое нагретое тело, находящееся в среде с температурой a. Согласно закону остывания (излучения тепла) Ньютона скорость охлаждения тела (в среде с температурой a) пропорциональная разности между температурой тела и температурой окружающей среды.
Если через x(t)
обозначить температуру тела в момент
времени t,
то процесс остывания можно выразить
дифференциальным уравнением
.
В частности, считая
температуру среды
(в некоторой шкале), получим уравнение
.
Если
–
есть начальная температура тела, то как
и в случае уравнения распада получаем
решение
.
3. Рассмотрим пример геометрической задачи, решение которой сводится к решению дифференциального уравнения:
Найти кривую, обладающую тем свойством, что отрезок любой ее касательной, заключенной между осями координат, делится пополам в точке касания.
Решение.
Пусть
- уравнение искомой кривой. Как известно,
уравнение касательной
или
.
По условию точка
или
принадлежит касательной. Следовательно,
или
,
т.е. получили дифференциальное уравнение.
Проверкой можно убедиться, что общее
решение
.
3.Теорема Коши для ду первого порядка
Функция
удовлетворяет условию Липшица
по переменной
на множестве
пространства переменных
,
если
.
(1)
Число
называется постоянной
Липшица.
Задача Коши для дифференциального уравнения первого порядка - это система, состоящая из уравнения
(2)
или
и
начального условия
,
(3)
т.е. состоит в
отыскании решения
,
удовлетворяющего уравнению (2) и начальному
условию (3).
Теорема
(Коши для дифференциального уравнения
первого порядка). Если в дифференциальном
уравнении (2) функция
удовлетворяет следующим двум условиям:
1)
непрерывна в
:
;
и, следовательно,
;
(4)
2) в имеет ограниченную по модулю частную производную по второму аргументу
;
(5)
то существует
единственное решение
задачи Коши (2), (3).
Доказательство. Покажем, что решение задачи Коши (2), (3) равносильно решению некоторого интегрального уравнения.
В самом деле, пусть
-
решение уравнения (2), заданное на
некотором интервале
и удовлетворяющее начальному условию
(3). Тогда при любом
имеет место тождество
.
(6)
Интегрируя тождество
(6) по
и учитывая равенство (3), получим
.
Очевидно и обратное утверждение: если непрерывная функция задана на интервале и удовлетворяет интегральному уравнению
, (7)
то ввиду непрерывности
имеем
,
,
то есть
есть решение уравнения (2), удовлетворяющее
начальному условию (3).
Таким образом, решение задачи Коши (2), (3) равносильно отысканию непрерывного решения интегрального уравнения (7) или неподвижной точки интегрального оператора вида (7).
Пусть
,
(8)
где постоянная
из
(4). Мы сможем гарантировать существование
решения задачи Коши (2), (3) на
,
а не на
.
Из условия (5) и теоремы о среднем:
,
где
,
следует справедливость условия Липшица
(1) для
.
По методу
последовательных приближений возьмем
в качестве нулевого приближения
постоянную функцию. Первым приближением
будет
.
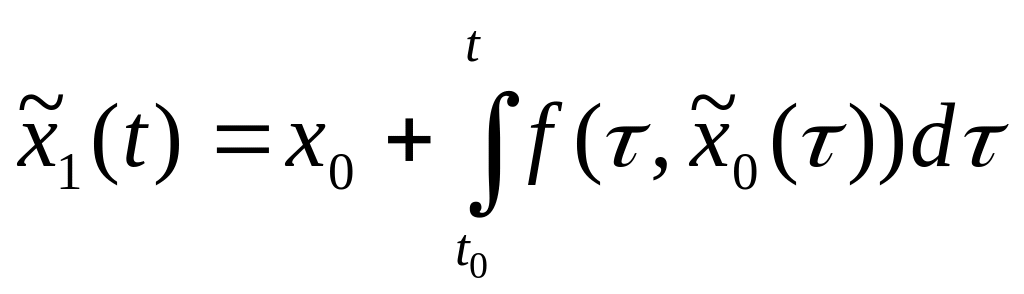Продолжая этот процесс, получим
.
(9)
Доказательство разобьем на 4 части.
1) Последовательность
приближений
из
(9)
не выходит за пределы
при
,
где
из (8).
Действительно, в силу (4) и (8) имеем
.
Методом индукции получим
.
2) Существует предел
.
(10)
Рассмотрим ряд
. (11)
Заметим, что
.
Отсюда, учитывая условие Липшица,
.
По методу индукции
предполагаем, что
.
Следовательно,
Таким
образом, члены функционального ряда
(11) из непрерывных функций, начиная с
,
мажорируем сходящимся числовым рядом
.
Поэтому по признаку Вейерштрасса ряд
(11) сходится равномерно на
к непрерывной функции
.
3) Функция
удовлетворяет интегральному уравнению
(7). Другими словами, в (9) можно перейти
к пределу под знаком интеграла. Так как
сходится
к
равномерно
и
непрерывна, то и
сходится
к
равномерно, но при равномерной сходимости
возможен предельный переход под знаком
интеграла.
4) Решение
единственно.
Пусть вопреки утверждению существует,
помимо
,
еще одно
решение
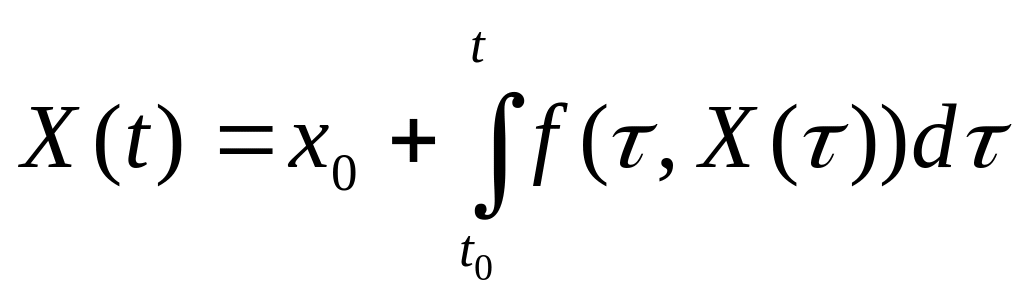.Отсюда
.
Следовательно, в силу условия Липшица
.
Рассмотрим значение
,
удовлетворяющее неравенству
.
Возьмем максимальное значение левой и
правой частей при таких
.
Получим противоречивое неравенство,
так как
и
.
Замечание.
Если условия теоремы Коши не выполнены,
то единственности может не быть. Например,
задача Коши
имеет бесконечно много решений: для
каждого
все решения
а
также
.
Здесь не выполнено условие теоремы Коши относительно непрерывности производной по зависимой переменной .