23. Функция Ляпунова. Теорема Четаева о неустойчивости

Теорема Четаева (о неустойчивости). Если существует дифференцируемая функция , называемая функцией Ляпунова, удовлетворяющая в некоторой замкнутой -окрестности начала координат условиям:

а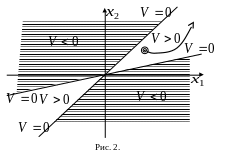 ) и в сколь угодно малой окрестности начала координат имеются точки, в которых .

б) В области производная взятая вдоль интегральной кривой , причем в области , , производная , то точка покоя системы (1) неустойчива.

Доказательство. Начальную точку возьмем в сколь угодно малой окрестности начала координат в области . Пусть . Так как по условию б) производная , то функция вдоль траектории не убывает и, следовательно, пока траектория не покинет рассматриваемую - окрестность начала координат траектория должна находиться в области . Допустим, что траектория не покидает - окрестность начала координат. Тогда

,

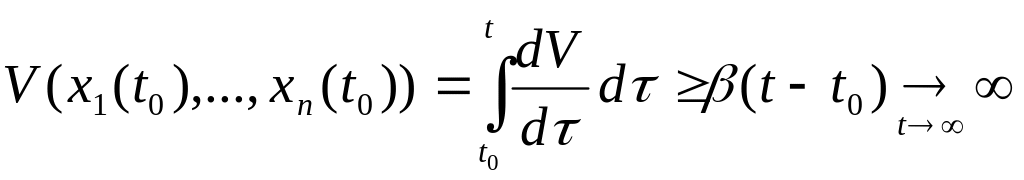что противоречит ограниченности непрерывной функции в замкнутой -окрестности начала координат. 

Пример. Исследовать на устойчивость тривиальное решение , системы

Решение. Пусть функция Ляпунова . Тогда , если , т.е. условие а) теоремы Четаева выполнено.

Для проверки выполнения условия б) вычисляем

.

Отсюда , если . Более того, в области , для любого найдется такое число , что производная , т.е. условие б) теоремы Четаева тоже выполнено.

Ответ: тривиальное решение , неустойчиво.

Исследовать на устойчивость тривиальное решение , :

1. 2. 3. 4.

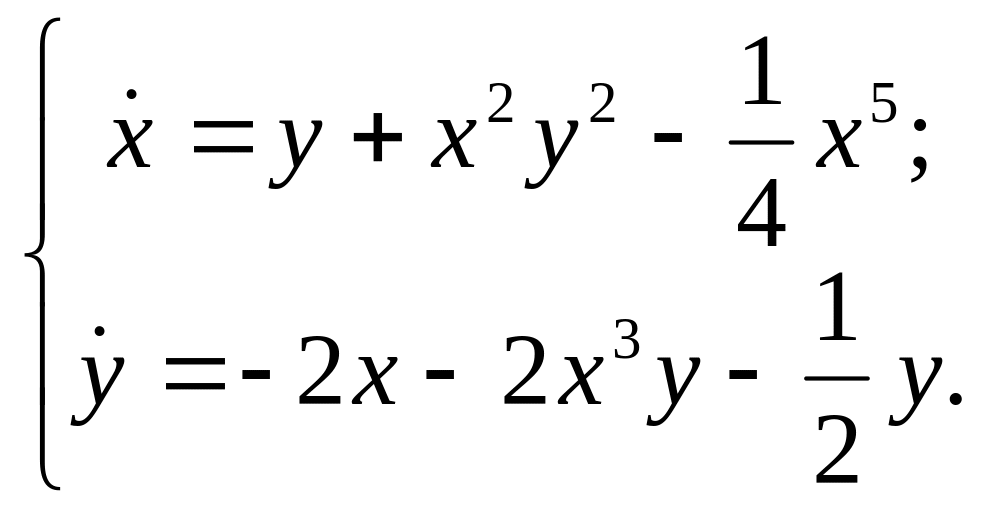
5.

Ответы: 1. . Неустойчива. 2. . Асимптотически устойчива. 3. . Неустойчива. 4. . Асимптотически устойчива.

5. . Неустойчива.

Приложение 1

Таблица основных интегралов

1. ; 2. ;3. ;

4. ; 5. ; 6. ;

7. ; 8. ;

9. ;10. ;

11. ; 12. ;

13. ; 14. ;

15. .

Приложение 2.

Тест

Не производя вычислений, необходимо выбрать правильный ответ или ответить на вопрос.

1. Какое из утверждений для числа особых решений уравнения верно: число особых решений уравнения равно а) двум; б) одному; в) нет особых решений?

2. Какое из утверждений для порядка уравнения верно: порядок дифференциального уравнения равен а) двум; б) одному; в) трем?

3. Пусть - общий интеграл дифференциального уравнения,

- константы. Какое из утверждений для порядка уравнения верно: порядок дифференциального уравнения равен а) двум; б) одному; в) трем?

4. Выполняются ли предположения теоремы Коши для уравнения на интервале ?

5. Линейная комбинация решений дифференциального уравнения является решением уравнения: а) всегда; б) для линейного однородного уравнения с постоянными коэффициентами; в) для любого линейного однородного уравнения;

г) для линейного неоднородного уравнения с постоянными коэффициентами;

д) для любого линейного неоднородного уравнения?

6. Пусть определитель Вронского системы функций равен 0. Какое из утверждений для системы функций верно: а) линейно зависима; б) линейно независима; в) ничего нельзя сказать о линейной зависимости или линейной независимости системы функций?

7. Какие из систем функций линейно независимы: а) , ; б) , ; в) , ?

8. Общее решение линейного неоднородного уравнения есть сумма … и …. Вставьте пропущенные слова из списка: а) частного решения однородного уравнения; б) общего решения однородного уравнения; в) частного решения неоднородного уравнения; г) общего решения неоднородного уравнения.

9. Определить типы дифференциальных уравнений: 1) ;

2) ; 3) ; 4) ;

5) , выбрав нужный ответ из списка: а) уравнение, допускающее понижение порядка; б) уравнение в полных дифференциалах; в) линейное неоднородное уравнение порядка выше 1; г)уравнение Эйлера; д) линейное однородное уравнение порядка выше 1.

9. Определите типы дифференциальных уравнений: 1) ; 2) ; 3) ; 4) ; 5) , выбрав нужный ответ из списка:

а) Риккати; б) с разделяющимися переменными; в) однородное; г) Бернулли;

д) Клеро.

10. Установите соответствие между уравнениями: 1) ;

2) ; 3) и заменами, с помощью которых они решаются: а) ; б) ; в) .