21. Функция Ляпунова. Теорема Ляпунова об устойчивости
Т
еорема
Ляпунова
(об устойчивости). Если существует
дифференцируемая функция
,
называемая функцией
Ляпунова,
удовлетворяющая в окрестности начала
координат следующим условиям:
а)
,
причем
лишь при
,
т.е. функция
имеет строгий минимум в начале координат.
б)
;
то точка покоя системы (18.1) устойчива.
Доказательство.
Заметим, что производная
в условии б) взята вдоль интегральной
кривой, т.е. она вычислена в предположении,
что переменные
функции
заменены решениями
системы дифференциальных уравнений
(1).
Действительно,
при этом предположении
или, заменяя
правыми частями системы (1), окончательно
получим
.
В окрестности
начала координат, как в окрестности
всякой точки строгого минимума,
поверхности уровня
функции
являются замкнутыми поверхностями,
внутри которых находится точка минимума
– начало координат. Зададим
.
При достаточно малом
поверхность уровня
целиком лежит в
-
окрестности начала координат, но не
проходит через начало координат,
следовательно, можно выбрать
,
такое, что
-
окрестность начала координат целиком
лежит внутри поверхности
,
причем в этой окрестности
.
Если начальная точка с координатами
выбрана в
-
окрестности начала координат и,
следовательно,
,
то при
точка траектории, определяемой этими
начальными условиями, не может выйти
за пределы
-
окрестности начала координат и даже за
пределы поверхности уровня
,
так как в силу условия б) теоремы функция
вдоль траектории не возрастает и,
следовательно, при
.
Замечание.
Общего метода построения функций
Ляпунова не существует. В простейших
случаях ее следует искать в виде:
,
,
,
подбирая надлежащим
образом постоянные
и
.
Пример.
Исследовать на устойчивость тривиальное
решение
,
системы
Решение.
Пусть функция Ляпунова
.
Тогда условие а)
теоремы Ляпунова выполнено. Для проверки
выполнения условия б) вычисляем
.
Отсюда условие б) тоже выполнено.
Тривиальное решение
,
устойчиво.
Пример.
Исследовать на устойчивость тривиальное
решение
,
системы
Решение.
Пусть функция Ляпунова
.
Тогда условие а)
теоремы Ляпунова выполнено. Для проверки
выполнения условия б) вычисляем
.
Отсюда
,
т.е. условие б) тоже выполнено. Тривиальное
решение
,
устойчиво.
22. Теорема Ляпунова об асимптотической устойчивости
Теорема Ляпунова (об асимптотической устойчивости). Если существует дифференцируемая функция , называемая функцией Ляпунова, удовлетворяющая в окрестности начала координат следующим условиям:
а) , причем лишь при , т.е. функция имеет строгий минимум в начале координат.
б) ;
причем вне сколь угодно малой окрестности начала координат, т.е. при
,
,
производная
,
где
-
постоянная, то точка покоя
системы (1)
асимптотически
устойчива.
Доказательство.
Так как условия теоремы об устойчивости
выполнены, то для любого
можно выбрать
,
такое, что траектория, начальная точка
которой находится в
-
окрестности начала координат, при
не выходит
за пределы
-
окрестности начала координат.
Следовательно, в частности, вдоль такой
траектории при
выполнено
условие б)
теоремы, поэтому функция
монотонно убывает с возрастанием
,
и вдоль траектории существует предел
функции
при
.
Надо доказать, что
,
так как если
,
то из условия а) следует, что
,
т.е. точка покоя
системы (1)
асимптотически устойчива.
Допустим, что
;
тогда траектория при
находится
в области
.
Следовательно, траектория находится
вне некоторой
-
окрестности начала координат
,
т.е. там, где по условию б)
при
.
Умножая
неравенство
на
и интегрируя вдоль траектории в пределах
от
до
,
получим
или
.
При достаточно
большом
правая часть отрицательна, а, следовательно,
и
,
что противоречит условию а).
Пример.
Исследовать на устойчивость тривиальное
решение
,
системы
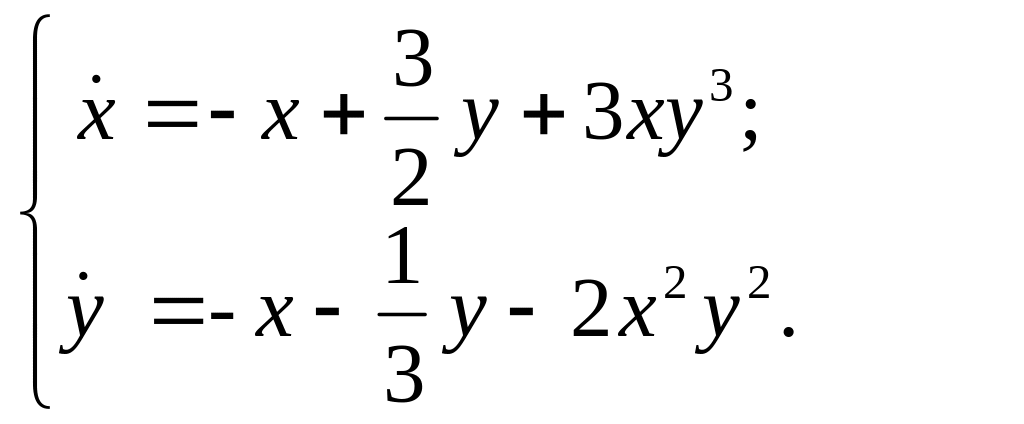
Решение.
Функцию Ляпунова будем искать в виде
,
,
.
Вычисляем
;
.
Отсюда, если
,
то
для каждого
,
т.е. условия теоремы Ляпунова об
асимптотической устойчивости выполнены.
Ответ: тривиальное решение , асимптотически устойчиво.