19. Простейшие типы точек покоя. Вещественные собственные значения

Рассмотрим автономную систему с постоянными коэффициентами

, - начальные условия, -

характеристическое уравнение с вещественными корнями .

Общее решение . Поэтому где

, , .

Отсюда , и частные решения:

,

.

В случае отрицательных вещественных собственных значений , можно выбрать и столь малыми, что для всех будет и , так как , (устойчивость) и, более того, , (асимптотическая устойчивость). В таблице 1 приведена классификация точек покоя.

Пример. Определить характер и исследовать на устойчивость точку покоя системы , (a, b  0).

Решение. Точка покоя - нулевое решение. Из системы находим

Траекторию фазовой кривой легко найти, исключая t из этой системы (x / a)² = y / b, т.е. y = kx² – парабола, где .

Ответ: Точка покоя - неустойчивый узел.

Пример. Определить характер и исследовать на устойчивость точку покоя системы , (a, b,  0).

Решение. Точка покоя - нулевое решение. Из системы находим

Траекторию фазовой кривой находим, исключая t из этой системы:

, т.е. y = kx² – парабола (a, b  0). Нулевое решение асимптотически устойчиво.

Ответ: Точка покоя - устойчивый узел.

Пример. Определить характер и исследовать на устойчивость точку покоя системы , (a, b  0).

Решение. Точка покоя - нулевое решение. Из системы находим

Уравнение траекторий получим исключением t, заметив, что - постоянная. Следовательно, y = k / x – гипербола.

Ответ: Седло. Точка покоя неустойчива.

Действительный корень кратности 2: , , - начальные условия, - характеристическое уравнение имеет один действительный корень кратности 2: . Следовательно, , , . Пусть . Тогда .

Поэтому .

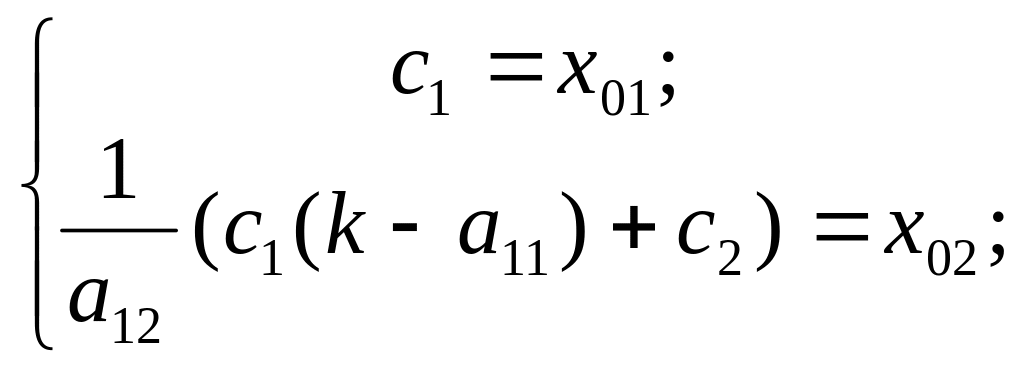
В случае отрицательного вещественного собственного значения (корня) , можно выбрать и столь малыми, что для всех будет и , так как и, более того, . Поэтому , , т.е.нулевое решение асимптотически устойчиво. В таблице 2 приведена классификация точек покоя.

Замечание. Если , , то точка покоя устойчива, асимптотической устойчивости нет. Если , , то точка покоя неустойчива.

В таблицах 1 и 2 приведена классификация точек покоя.

20. Простейшие типы точек покоя. Комплексные собственные значения

Рассмотрим автономную систему с постоянными коэффициентами:

, - начальные условия, -

характеристическое уравнение с комплексными сопряженными корнями . Заметим, что . Отсюда ,

, , ,

,

.

Поэтому .

Следствие. Если все корни характеристического уравнения системы имеют отрицательную действительную часть, то точка покоя системы асимптотически устойчива. Если же хотя бы один из корней характеристического уравнения имеет положительную действительную часть, то точка покоя не устойчива. В таблице 3 приведена классификация точек покоя.

Пример. Определить характер и исследовать на устойчивость точку покоя системы , (a, b,  0).

Решение. Находим корни характеристического уравнения . Отсюда , ,

Поэтому . Система имеет решение

Пусть , , , . Тогда или

В полярных координатах получили семейство логарифмических спиралей. Тривиальное решение асимптотически устойчиво.

Ответ: точка покоя –устойчивый фокус.

Таблица 3

Корни ,		Характер точки покоя	Устойчивость точки покоя
Комплексные ,	,	Устойчивый фокус	Асимптотически устойчива
	,	Неустойчивый фокус	Неустойчива
	,	Центр	Устойчива

Пример. Определить характер и исследовать на устойчивость точку покоя системы , (a, b,  0) .

Решение. Характеристическое уравнение имеет чисто мнимые корни . Отсюда , ,

Поэтому . Система имеет решение

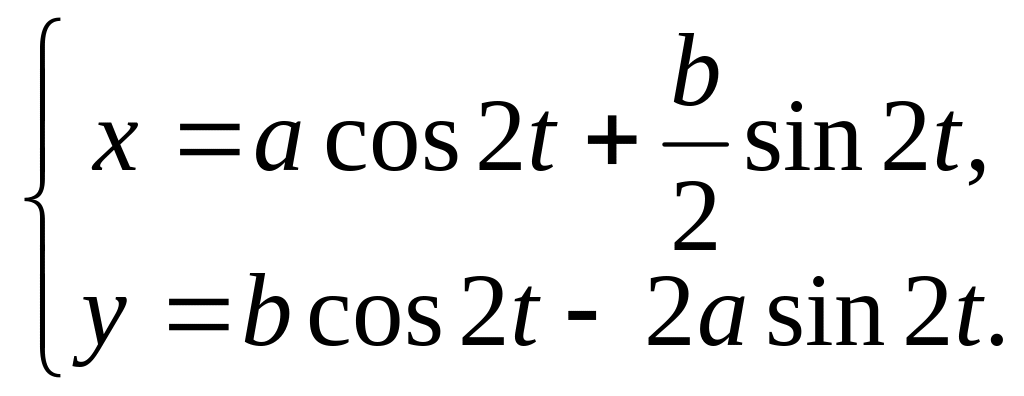
Отсюда или 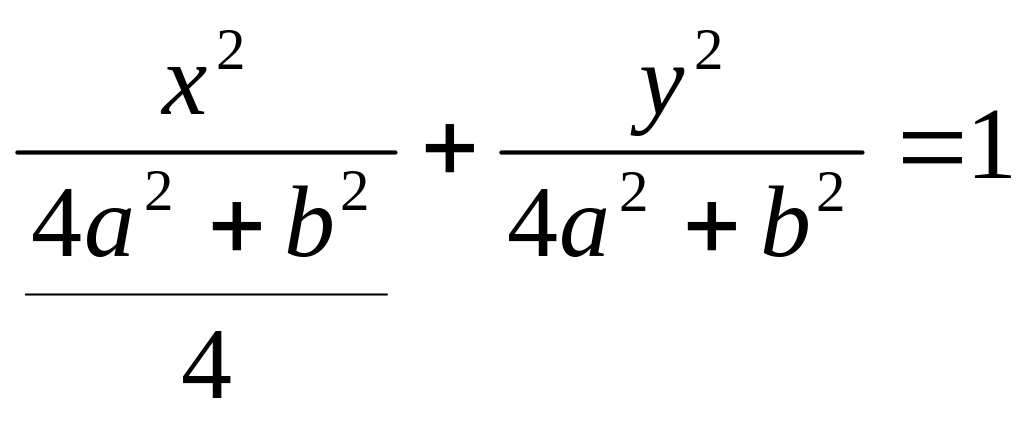(уравнение эллипса).

Ответ: точка покоя – устойчивый центр, асимптотической устойчивости нет.

Предположим, что правые части системы дифференцируемы в начале координат достаточное число раз. Разложим по формуле Тейлора в окрестности начала координат:

(8)

где , - члены второго порядка малости относительно и при , .

Система - система по первому приближению для (8).

Пример. Исследовать на устойчивость по первому приближению точку покоя системы

Решение. Для системы по первому приближению находим корни характеристического уравнения .

Ответ: точка покоя асимптотически устойчива.

Задачи для самостоятельного решения:

Исследовать на устойчивость по первому приближению точки покоя следующих систем:

1. 2. 3.

4. 5. 6.

Ответы: 1. Устойчива. 2. Не устойчива. 3. Не устойчива. 4. Устойчива.

5. Устойчива. 6. Не устойчива.