22Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке

Говорят, что функция   , определенная на промежутке Х, достигает на нем своего наибольшего (наименьшего) значения, если существует точка а, принадлежащая этому промежутку, такая, что для всех х из Х выполняется неравенство   .

Функция, непрерывная на отрезке, достигает на нем своего наибольшего и наименьшего значений.

Наибольшее значение М и наименьшее значение m непрерывной функции могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка является точкой экстремума.

Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции   на отрезке   :

1. найти  ;

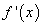2. найти точки, в которых 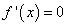  или   не существует, и отобрать из них те, что лежат внутри отрезка  ;

3. вычислить значения функции   в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции   на отрезке   , которые можно обозначить так:  .

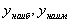Если поставлена задача найти   для непрерывной на   функции   , то она решается по тому же правилу, что соответствующая задача для отрезка   .

Отличие: на третьем этапе вместо вычисления значений функции на концах отрезка находят пределы функции при приближении к концам интервала.

Иногда для отыскания наибольшего или наименьшего значения непрерывной функции  на промежутке   полезны два утверждения:

1. если функция   имеет в промежутке Х только одну точку экстремума 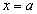 , причем это точка максимума, то   - наибольшее значение функции на промежутке Х;

2. если функция   имеет в промежутке Х только одну точку экстремума  , причем это точка минимума, то   - наименьшее значение функции на промежуткеХ.

23.

24. Асимптота

• Аси́мпто́та^[1] (от греч. ασϋμπτωτος — несовпадающий, не касающийся) кривой с бесконечной ветвью — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность^[2]. Термин впервые появился уАполлония Пергского, хотя асимптоты гиперболы исследовал ещё Архимед^[3].

Виды асимптот графиков ]Вертикальная

Вертикальная асимптота — прямая вида   при условии существования предела  .

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

1. 

2. 

Замечание: обратите внимание на знаки бесконечностей в этих равенствах.

]Горизонтальная

Горизонтальная асимптота — прямая вида   при условии существования предела

.

]Наклонная

Наклонная асимптота — прямая вида   при условии существования пределов

Пример наклонной асимптоты

1. 

2. 

Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот!

Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен  ), то наклонной асимптоты при  (или  ) не существует!

Связь между наклонной и горизонтальной асимптотами

Если при вычислении предела  , то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?

Дело в том, что горизонтальная асимптота является частным случаем наклонной при  , и из выше указанных замечаний следует, что

1. Функция имеет или только одну наклонную асимптоту, или одну вертикальную асимптоту, или одну наклонную и одну вертикальною, или две наклонных, или две вертикальных, либо же вовсе не имеет асимптот.

2. Существование указанных в п. 1.) асимптот напрямую связано с существованием соответствующих пределов.

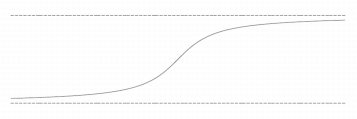
График функции с двумя горизонтальными асимптотами

]Нахождение асимптот

[Порядок нахождения асимптот

1. Нахождение вертикальных асимптот.

2. Нахождение двух пределов 

3. Нахождение двух пределов  :

если   в п. 2.), то  , и предел   ищется по формуле горизонтальной асимптоты,  .

[]Наклонная асимптота — выделение целой части

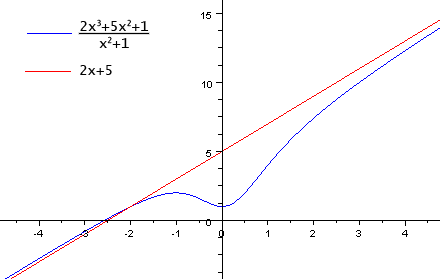
Также наклонную асимптоту можно найти, выделив целую часть. Например:

Дана функция  .

Разделив нацело числитель на знаменатель, получим:

.

При    ,    ,   то есть:

,

и   является искомым уравнением асимптоты.

25. Первообразная

Первообра́зной^[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Так, например, функция   является первообразной  . Так как производная константы равна нулю,   будет иметь бесконечноеколичество первообразных; таких как   или   … и т. д.; таким образом семейство первообразных функции   можно обозначить как  , где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.

Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:

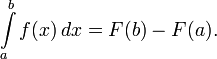
Это соотношение называется формулой Ньютона — Лейбница.

Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:

Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.

Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:

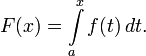
Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например,   с   не непрерывна при  , но имеет первообразную   с  .

Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены,экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:

Более развёрнутое изложение этих фактов см. в дифференциальной теории Галуа.