13Дифференцирование функций заданных параметрически

  До сих пор функция записывалась в явном виде y= f(x) и в неявном F(x,y)=0. Но существует еще третий вид аналитического представления функции - это представление её в па раметрической форме в виде двух уравнений

где t - вспомогательная переменная, называемая параметром.   Заметим, что функция может быть представлена в параметрической форме различными способами.   Например, функция, записанная в неявном виде x² + y² = 1 может быть представлена в явном виде:   и в параметрической форм е:

  Заметим, что x² + y² = 1 есть уравнение окружности единичного радиуса с центром в начале координат.   В первом параметрическом представлении уравнения x² + y² = 1 параметр t изменяется от -1 до +1 и равен абциссе подвижной точки окружности, во втором случае параметр t изменяется от 0 до 2p и равен углу, образованному радиусом подвижной точки и осью Ox.   Если функция задана в явном виде y=f(x), то всегда можно записать её в неявном виде y-f(x)=0, а также в параметрической форме

От вида F(x,y)=0 не всегда возможно перейти к виду y=f(x) или x=(y), так как уравнение F(x,y)=0 может оказаться неразреш имым относительно y или x .   Лего перейти от параметрического представления функции к уравнению вида y=f(x). Для этого из первого уравнения x=x(t) нужно найти t=t(x), если конечно это возможно , и подставить его во второе уравнение y=y(t)

y=y[t(x)]=f(x)

   От параметрического представления функции к уравнению вида F(x,y)=0 можно прийти путем исключения параметра t, если это возможно.    Уравнения y=f(x) и F(x, y)=0 служат различными аналитическими представлениями одной и той же функции F[x, f(x)]=0. Параметрические уравнения

и уравнение F(x, y)=0 представляют одну и ту же функцию, если F(x(t), y(t))=0.    Наконец, параметрические уравнения определяют ту же функцию, что и уравнение y=f(x), если

y(t)=f [ x(t) ].

   Найдем производную функции y по x в случае, когда она задана в параметрическом виде. Для этого будем рассматривать t как функцию от x. То есть t=t(x). Тогдаy=y[t(x)]. Продифференцируем y как сложную функцию от x, т.е. по формуле

и применим формулу, связывающую производные обратных функций:

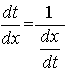
   Введя обозначения

,       

получим

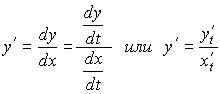
Пример.    

   Теперь найдем вторую производную от функции, заданной в параметрической форме.    Из предидущего уравнения и определения второй производной следует, что

   но

   Следовательно

   где

              

14. Теорема Ролля

Теорема Ро́лля (теорема о нуле производной) утверждает, что

Если вещественная функция непрерывна на отрезке   и дифференцируема на интервале  , принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

Доказательство  

Геометрический смысл теоремы Ролля

]Геометрический смысл

Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.

]Следствие

Если непрерывная функция обращается в ноль в   различных точках, то ее производная обращается в ноль по крайней мере в   различных точках^[1], причем эти нули производной лежат в выпуклой оболочке нулей исходной функции. Это следствие легко проверяется для случая действительных корней, однако имеет место и в комплексном случае.

15. Теорема Лагранжа (теория групп)

Теорема Лагра́нжа в теории групп гласит:

Пусть группа G конечна и H — её подгруппа. Тогда порядок G равен порядку H, умноженному на количество её левых или правыхклассов смежности (индекс).

Следствия

1. Количество правых и левых смежных классов любой подгруппы   в 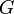  одинаково и называется индексом подгруппы   в   (обозначается  ).

2. Порядок любой подгруппы конечной группы   делит порядок  .

3. Из того, что порядок элемента группы равен порядку циклической подгруппы, образованной этим элементом, следует, что порядок любого элемента конечной группы   делит порядок  . Это следствие обобщает теорему Эйлера и малую теорему Ферма в теории чисел.

4. Группа порядка  , где   — простое число, циклична. (Поскольку порядок элемента, отличного от единицы, не может быть равен 1, все элементы, кроме единицы, имеют порядок  , и значит, каждый из них порождает группу.)