8 Дифференцируемость сложной функции
Рассмотрим сложную функцию y = y(u(x))
Теорема 4. Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y'u, u'x), тогда сложная функция y = y(u(x)) дифференцируема и y'x = y'u u'x.
Доказательство
Если аргумент x получит приращение Δx, то функция u получит приращение Δu = u(x + Δx) − u(x), а функция y получит приращение Δy = y(u + Δu) − y(u). Но тогда, воспользовавшись свойствами предела функции, получаем
Теорема доказана.
9 Инвариантность формы дифференциала
Рассмотрим
сложную функцию y=f(u(x)).
Пусть функции y=f(u),
u=u(x)
дифференцируемы, тогда
Таким образом, если аргументом функции является функция другого аргумента, то форма дифференциала совпадает с формой дифференциала dy = f'(x)dx, когда аргументом функции является независимая переменная. Это свойство называется инвариантностью формы дифференциала.
10 Понятие обратной функции. Производная обратной функции
Функция
называется
обратимой,
если для любых двух различных чисел
и
,
принадлежащих
,
числа
и
также
различны.
Пример
1.
Пример
2.
.
Пример
3.
.
Пример
4.
.
Пример
5.
.
Пример
6.
.
ф
Рассмотрим функцию y = f(x), для которой существует обратная функция x = g(y).
Теорема
5. Если обратная функция x
= g(y)
дифференцируема и g'(y)
≠
0,
то функция y=f(x)
дифференцируема, и
Доказательство
Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом: Δx=g(y + Δy) − g(y).
Тогда получаем
Теорема доказана.
11.Применение дифференциала в приближенных вычислениях
Пусть нам известно значение функции y0=f(x0) и ее производной y0' = f '(x0) в точке x0. Покажем, как найти значение функции в некоторой близкой точке x. Как мы уже выяснили приращение функции Δyможно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f'(x0)·Δx. Т.к., по определению, Δy = f(x) – f(x0), то f(x) – f(x0)≈f'(x0)·Δx. Откуда f(x) ≈ f(x0) + f'(x0)·Δx
12. Дифференциал высшего порядка
ля
функции, зависящей от одной переменной 
второй и третий дифференциалы выглядят
так:
Отсюда можно вывести общий вид дифференциала n-го порядка от функции :
При
вычислении дифференциалов высших
порядков очень важно, что 
есть
произвольное и не зависящее от 
,
которое при дифференцировании по
следует рассматривать как постоянный
множитель.
[править]Дифференциал высшего порядка функции нескольких переменных
Если
функция 
имеет непрерывные частные производные
второго порядка, то дифференциал второго
порядка определяется так: 
.
Символически
общий вид дифференциала n-го
порядка от функции 
выглядит
следующим образом:
где 
,
а 
произвольные
приращения независимых
переменных 
.
Приращения
рассматриваются как постоянные и
остаются одними и теми же при переходе
от одного дифференциала к следующему.
Сложность выражения дифференциала
возрастает с увеличением числа переменных.
[править]Неинвариантность дифференциалов высшего порядка
При
, 
-й
дифференциал не инвариантен (в отличие
от инвариантности
первого дифференциала),
то есть выражение 
зависит,
вообще говоря, от того, рассматривается
ли переменная
как
независимая, либо как некоторая
промежуточная функция другого переменного,
например, 
.
Для
доказательства неинвариантности
дифференциалов высшего порядка достаточно
привести пример.
При n
= 2 и
:
если — независимая переменная, то
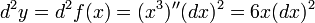
есл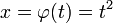и
и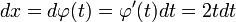 
при этом,
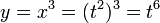и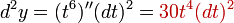 
С
учётом зависимости 
,
уже второй дифференциал не обладает
свойством инвариантности при замене
переменной. Также не инвариантны
дифференциалы порядков 3 и выше.