41. Интегрирование по частям

Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы

для неопределённого интеграла:

для определённого:

Предполагается, что нахождение интеграла   проще, чем  . В противном случае применение метода неоправдано.

]Получение формул ]Для неопределённого интеграла

Функции   и   гладкие, следовательно, возможно дифференцирование:

Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:

Операция интегрирования обратна дифференцированию:

После перестановок:

Не стоит, однако, забывать, что это равенство подразумевается в смысле равенства множеств, то есть, грубо говоря, с точностью до константы, возникающей во время интегрирования.

Типичную ошибку «потери» константы при обращении с неопределенным интегралом иллюстрирует следующий пример-софизм:

Отсюда «следствие»:  , что очевидно неверно.

]Для определённого интеграла

В целом аналогично случаю неопределённого интеграла:

]Примеры

• Иногда этот метод применяется несколько раз:

• Данный метод также используется для нахождения интегралов от элементарных функций:

• В некоторых случаях интегрирование по частям не даёт прямого ответа:

Таким образом один интеграл выражается через другой:

Решив полученную систему, получаем:

42. Вычисление площадей плоских фигур

В прямоугольной системе координат площадь ограниченной правильной в направлении оси ОХ области      равна

43. Вычисление площади плоской фигуры

б) Площадь плоской фигуры в полярных координатах

На плоскости можно рассмотреть полярную систему координат  . Тогда точке   соответствуют координаты   и  , предполагаем полуоси   и   ( ) совпадающими; причем    положительное  направление угла    – против вращения часовой стрелки.

Ф игура на плоскости, ограниченная лучами  ,   ( ) и кривой  ,  , называется криволинейным сектором. Очевидно, при    имеет круговой сектор и его площадь  . Поэтому если провести процедуру построения интегральной суммы   для разбиения  ,  ,   и системы точек  , то при  , где  ,  , придем к интегралу  , который можно  интерпретировать как площадь криволинейного сектора.

Итак, если предел интегральной суммы, построенной по указанной процедуре, существует, то площадь криволинейного сектора можно вычислить по формуле

.

П РИМЕР 7. Найти площадь фигуры, ограниченной лемнискатой  Бернулли   и окружностью   (внутри  окружности).

Решение. Лемниската существует при  , т.е. для   или для  ; периодически повторяется для  . Симметрия кривой следует из четности функции  . При  , изменяющемся от   до  , значение   убывает от   до  , т.е. значение   убывает от   до   ( ) (см. рисунок). Пересечение лемнискаты и окружности 

  имеем при   и по  симметрии при  .

Для вычисления площади используем симметрию фигуры  ;   – площадь фигуры в I квадранте. Фигура   – объединение двух криволинейных секторов и поэтому

.

Окончательно имеем  .

44. Формулы объема геометрических тел

 

Расчет объема куба

 

 

a - сторона куба

 

 

Формула объема куба, (V ):

 

 

Объем прямоугольного параллелепипеда

 

 

a, b, c- стороны параллелепипеда

 

 

Формула объема параллелепипеда, (V):

 

 

Формула вычисления объема шара

 

 

R- радиус шара

π≅ 3.14

 

 

Объем шара, (V):

 

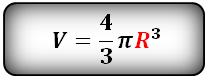
Объем шарового слоя

 

h- высота шарового слоя

R- радиус нижнего основания

r- радиус верхнего основания

π=3,14

 

Объем шарового слоя, (V):

 

 

Объем шарового сектора

 

 

h - высота сегмента

R - радиус шара

π=3,14

 

 

Объем шарового сектора, (V):

 

 

Объем шарового сегмента, формула

Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R - радиус шара

h - высота сегмента

π=3,14

 

 

 

Объем шарового сегмента, (V):

 

 

Как вычислить объем цилиндра ?

 

h- высота цилиндра

r- радиус основания

π ≅3,14

 

 

Объем цилиндра, (V):

 

 

Как найти объем конуса ?

 

H- высота конуса

R- радиус основания

π=3,14

 

Объем конуса, (V):

 

 

Формула объема усеченного конуса

 

R- радиус нижнего основания

r- радиус верхнего основания

h- высота конуса

π=3,14

Объем усеченного конуса,  (V ):

 

Объем конуса

Площадь поверхности конуса

Площадь поверхности усеченного конуса

 

Расчет объема пирамиды

 

 

h - высота пирамиды

S - площадь основания ABCDE

 

Объем пирамиды, (V):

 

Расчёт объёма усечённой пирамиды

 

h - высота пирамиды

S_ниж - площадь нижнего основания, ABCDE

S_верх - площадь верхнего основания, abcde

 

 

Объем усеченной пирамиды, (V):

 

 

Найти объем правильной пирамиды

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.

h - высота пирамиды

a - сторона основания пирамиды

n - количество сторон многоугольника в основании

 

 

Объем правильной пирамиды, (V):

 

 

Объем правильной треугольной пирамиды

Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.

h - высота пирамиды

a - сторона основания

 

Объем правильной треугольной пирамиды, (V):

 

 

Объем правильной четырехугольной пирамиды

Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.

h - высота пирамиды

a - сторона основания

 

 

 

Объем правильной четырехугольной пирамиды, (V):

 

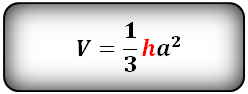
Объем тетраэдра

 

тетраэдр- пирамида у которой все грани, равносторонние треугольники.

а -ребро тетраэдра

Объем тетраэдра (V):

45. Длина кривой

Длина кривой (или, что то же, длина дуги кривой) в метрическом пространстве — числовая характеристика протяжённости этой кривой^[1]. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление). Если длина кривой существует и конечна, то говорят, что кривая спрямляемая, в противном случае — неспрямляемая.

]Определение

]Евклидово пространство

Для евклидова пространства длина отрезка кривой определяется как точная верхняя грань длин вписанных в кривую ломаных. Для наглядности рассмотрим трёхмерное пространство. Пусть непрерывная кривая   задана параметрически:

,

(1)

Приближение кривой ломаными

где  . Рассмотрим всевозможные разбиения интервала значений параметра   на   отрезков:  . Соединив точки кривой   отрезками прямых, мы получим ломаную линию. Тогда длина отрезка кривой определяется как точная верхняя грань суммарных длин всех таких ломаных.

Всякая непрерывная кривая имеет длину, конечную или бесконечную. Если все функции в (1) являютсяфункциями ограниченной вариации, то длина кривой существует и конечна. В математическом анализе выводится формула для вычисления длины  отрезка кривой, заданной уравнениями (1), при условии, что все три функции непрерывно дифференцируемы:

(2)

Формула подразумевает, что   и длина отсчитывается в сторону возрастания параметра t. Если рассматриваются два разных направления отсчёта длины от точки кривой, то часто удобно приписать дуге на одном из этих направлений знак минус.

В n-мерном случае вместо (2) имеем аналогичную формулу:

.

Можно также вычислить длину кривой   через криволинейный интеграл I рода: