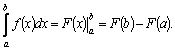39. Теорема Ньютона — Лейбница

Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.

Если непрерывна на отрезке и — ее любая первообразная на этом отрезке, то имеет место равенство

]История

Ещё до появления математического анализа данная теорема (в геометрической или механической формулировке) была известна Торричелли, Грегори иБарроу. Например, Барроу описал этот факт в 1670 году как зависимость между задачами на квадратуры и на проведение касательных. После созданияНьютоном и Лейбницем дифференциального и интегрального исчислений смысл формулы стал трактоваться чисто математически: операции дифференцирования и интегрирования взаимно обратны.

Ньютон сформулировал теорему словесно следующим образом: «Для получения должного значения площади, прилегающей к некоторой части абсциссы, эту площадь всегда следует брать равной разности значений z [первообразной], соответствующих частям абсцисс, ограниченным началом и концом площади». У Лейбница запись данной формулы в современном виде также отсутствует, поскольку обозначение определённого интеграла появилось гораздо позже, у Фурье в начале XIX века. Современное оформление и строгое доказательство впервые опубликованы также в начале XIX века Лакруа.

Формула Ньютона–Лейбница

Теорема. Если – какая–либо первообразная для непрерывной функции , то

Доказательство. Пусть –некоторая первообразная функции . Но – также первообразная для , а любые две первообразные данной функции отличаются на постоянную, то есть можно записать:

(4)

Это равенство справедливо для любых . Положим : Но , поэтому , . Полагая в (4) x=b и подставляя значение C, получим Переобозначив переменную интегрирования , получим формулу Ньютона – Лейбница:

При вычислении определенных интегралов будем записывать:

Пример1. (геометрически это площадь фигуры, ограниченной одной полуволной синусоиды и отрезком оси Ox).

Пример2.

40. Замена переменной в определенном интеграле

При вычислении определенных интегралов с использованием формулы Ньютона-Лейбница предпочтительно жестко не разграничивать этапы решения задачи (нахождение первообразной подынтегральной функции, нахождение приращения первообразной). Такой подход, использующий, в частности, формулы замены переменной и интегрирования по частям для определенного интеграла, обычно позволяет упростить запись решения.

ТЕОРЕМА. Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а=φ(α), в=φ(β) и функция f(х) непрерывна в каждой точке х вида х=φ(t), где t [α,β].

Тогда справедливо следующее равенство:

Эта формула носит название формулы замены переменной в определенном интеграле.

Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).

Пример 19. Вычислить