
- •1. Способы задания движения точки.
- •2. Определение скорости точки при задании ее движения векторным способом
- •3. Определение скорости точки при задании ее естественным способом.
- •4. Проекция на касательную к траектории.
- •5. Определение точки при задании ее координатным способом
- •6. Проекции скорости точки на неподвижные оси декартовых координат
- •7. Годограф скорости точки и его уравнения.
- •8. Прямолинейное движение, скорость и ускорение
- •9. Графическое представление закона движения точки.
- •10. Уравнения движения точки в декартовых координатах
- •11. Гармонические колебания.
- •12. Разложение скорости
- •13. Скорость в круговом движении. Угловая скорость
- •14. Закон равномерного, равнопеременного криволинейного движения
- •15. Секторная скорость.
- •16. Выражение скорости в криволинейных координатах.
- •18. Кривизна кривой. Радиус кривизны.
- •19.Проекции скоростей в ортогональной криволинейной системе координат.
- •20. Ускорение точки в криволинейной системе координат.
- •21 Скорость и ускорение точки в цилиндрической системе координат
- •22. Скорость и ускорение в сферической системе координат
- •23. Определение скорости точки в полярной системе координат
- •24. Поступательное движение твердого тела.
- •25. Теорема о перемещении тела, имеющего одну неподвижную точку. Угловая скорость тела.
- •26. Угловая скорость и угловое ускорение
- •27. Аксоиды мгновенных осей
- •28. Вращение вокруг неподвижной оси
- •29)Векторное выражение вращательной скорости и центростремительного ускорения.
- •30)Скорости и ускорения точек вращающегося тела.
- •31)Плоское движение твердого тела. Уравнения плоского движения.
- •32) Разложение плоского движения на поступательное движение вместе с полюсом и вращательное вокруг оси, проходящей через полюс.
- •33)Теорема об ускорении точек плоской фигуры и её следствие
- •34)План скоростей
- •36) Теорема о центре поворота для конечного перемещения плоской фигуры. Теорема Шаля
- •37)Теорема Эйлера-Даламбера:
- •38)Определение скоростей точек плоской фигуры с помощью мцс.
- •39)Мгновенный центр ускорений.
- •40)Векторные и скалярные формулы для скоростей и ускорений точек тела при его вращ.Вокруг неподвижной точки.
- •41) Свободное движение твердого тела. Скорости и ускорения его точек.
- •42) Относительное, переносное и абсолютное движение точки.
- •43) Сложное движение точки. Основные понятия и определения. Примеры.
- •44) Полная и относительная производная от вектора.
- •45. Сложное движение точки. Теорема о сложении скоростей.
- •49) Мгновенный центр ускорений.
- •50) Определение ускорений точек плоской фигуры
- •51) Сложение вращений вокруг двух параллельных осей
- •52) Основная теорема кинематики твердого тела (теорема о проекциях скоростей двух точек твердого тела на прямую, соединяющую эти точки).
- •53)В какой плоскости расположено ускорение точки и чему равны его проекции на естественные координатные оси?
- •54)Что характеризуют собой касательное и нормальное ускорение точки?
- •55)При каком движении точки равно нулю касательное ускорении и при каком нормальное?
- •56)Подвижные и неподвижные центроиды.
- •57. Напишите теорему Штейнера
- •58. Сложение мгновенных, угловых и поступательных скоростей.
- •59. Сложные поступательные движения.
- •60. Винтовое движение.
14. Закон равномерного, равнопеременного криволинейного движения
1)Если
во все время движения числена величина
скорости постоянна, т.е.
 ,
то криволинейное движение называется
равномерным. Из выражения
,
то криволинейное движение называется
равномерным. Из выражения
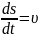 или
или
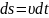 ,
интегрируя, найдем закон равномерного
криволинейного движения:
,
интегрируя, найдем закон равномерного
криволинейного движения:
 ,
(1)
,
(1)
где s0 – начальное расстояние точки(в момент t=0).
2)Если
касательное
ускорение точки
во все время движения постоянно, т.е.
 ,
то криволинейное движение называется
равнопеременным. Из выражения
,
то криволинейное движение называется
равнопеременным. Из выражения
 найдем закон изменения скорости в этом
движении:
найдем закон изменения скорости в этом
движении:
 ,
(2)
,
(2)
где
 - начальная скорость точки (в момент
t=0).
Отсюда, принимая во внимание, что
- начальная скорость точки (в момент
t=0).
Отсюда, принимая во внимание, что
 ,
получим закон равнопеременного
криволинейного движения в виде:
,
получим закон равнопеременного
криволинейного движения в виде:
 ,
(3)
,
(3)
где
s0
– начальное расстояние. От случая
прямолинейного движения выражение (3)
отличается тем, что в него вместо x
входит s,
а вместо a
– величина
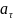 .
.
15. Секторная скорость.
Предположим, что точка М движется по закону: x=x(t); y=y(t); z=z(t). или в векторной форме, r=r(t).
Радиус-вектор
точки, перемещаясь в пространстве,
описывает конус, направляющей которого
служит траектория точки. Обозначим
величину площади О боковой поверхности этого конуса,
ограниченной кривой и двумя
радиусами-векторами r(
боковой поверхности этого конуса,
ограниченной кривой и двумя
радиусами-векторами r( )
и r(t),
через
)
и r(t),
через
 (рис
55).
(рис
55).
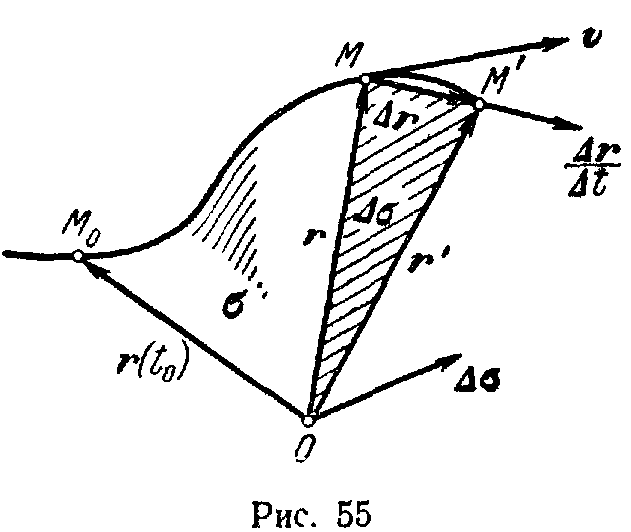
Пусть в момент
t+ t
приходит в положение М’, определяемое
радиус-вектором r’=
r(t+
t).
тогда, если
t
мало, то приращение площади
за промежуток времени
t
можно приближённо представить вектором,
изображающим плоскую площадку ОММ’,
т.е. вектором, модуль которого равен
половине площади параллелограмма,
построенного на векторах r
и
r=
r’-
r,
следовательно,
t
приходит в положение М’, определяемое
радиус-вектором r’=
r(t+
t).
тогда, если
t
мало, то приращение площади
за промежуток времени
t
можно приближённо представить вектором,
изображающим плоскую площадку ОММ’,
т.е. вектором, модуль которого равен
половине площади параллелограмма,
построенного на векторах r
и
r=
r’-
r,
следовательно,
 ОММ’=1/2(r*
r).
ОММ’=1/2(r*
r).
Предел отношения
приращения площади, описываемой
радиус-вектором, к соответствующему
промежутку времени
t,
при .
.
Чтобы найти
выражение
 через вектор скорости
через вектор скорости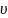 ,
разделим обе части равенства на
t
и получим:
,
разделим обе части равенства на
t
и получим:
 =
r*
=
r* .
.
Следовательно,
 =2
=2 r*
r* ,
т.е. удвоенная секторная скорость точки
относительно некоторого центра равна
моменту скорости этой точки относительно
того же центра. Из последней формулы
видно, что секторная скорость зависит
от центра, относительно которого она
определяется, и для каждого центра
будет иметь свою величину; поэтому,
задавая секторную скорость, необходимо
указывать центр, относительно которого
она берётся.
,
т.е. удвоенная секторная скорость точки
относительно некоторого центра равна
моменту скорости этой точки относительно
того же центра. Из последней формулы
видно, что секторная скорость зависит
от центра, относительно которого она
определяется, и для каждого центра
будет иметь свою величину; поэтому,
задавая секторную скорость, необходимо
указывать центр, относительно которого
она берётся.
16. Выражение скорости в криволинейных координатах.
Пусть в некоторой декартовой системе К точка М имеет координаты x,y,z. Всякой системе значений будет соответствовать определённая система значений (q1,q2,q3).(эти числа называются криволинейными координатами).
Чтобы
получить выражение скорости в
криволинейных координатах, проще всего
воспользоваться формулой:
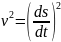 и найти в криволинейных координатах
выражение элемента дуги
и найти в криволинейных координатах
выражение элемента дуги
 .
Пусть имеем прямоугольную декартову
систему координат. Тогда
.
Пусть имеем прямоугольную декартову
систему координат. Тогда

Для
сферических координат, считая
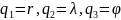 ,
найдем :
,
найдем :
 +
+
 .
.
В
сферических координатах скорость равна
:
 +
+ ².
².
Для
цилиндрических координат, полагая
 .
Получим, что
.
Получим, что

В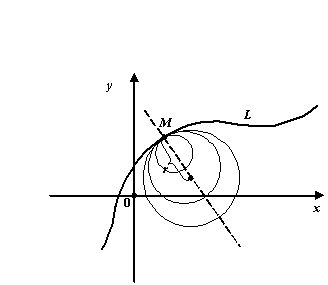 цилиндрических координатах :
цилиндрических координатах :

17.
Разложение
ускорения по осям естественного
трехгранника. Представим скорость
точки M
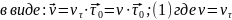 – проекция
вектора скорости
– проекция
вектора скорости
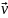 на ось
на ось
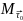 .
Дифференцируя равенство (1) по времени,
получим:
.
Дифференцируя равенство (1) по времени,
получим:
 .
Первое
слагаемое есть вектор
.
Первое
слагаемое есть вектор
 ,
направленный вдоль касательной
,
направленный вдоль касательной
 Найдем значение второго слагаемого.
Дифференциал единичного вектора
Найдем значение второго слагаемого.
Дифференциал единичного вектора
 перпендикулярен к
перпендикулярен к
 и лежит в соприкасающейся плоскости.
Следовательно, вектор
направлен по главной нормали
и лежит в соприкасающейся плоскости.
Следовательно, вектор
направлен по главной нормали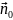 .
Кроме того, |
.
Кроме того, |
 | = |
|
⋅ dθ = dθ , где dθ – элементарный угол
смежности. Отсюда находим, что
=
dθ ⋅
и
| = |
|
⋅ dθ = dθ , где dθ – элементарный угол
смежности. Отсюда находим, что
=
dθ ⋅
и
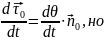 поскольку
поскольку
 и
и
 , (где ρ есть
радиус кривизны кривой в точке M ), и
тогда окончательно запишем:
, (где ρ есть
радиус кривизны кривой в точке M ), и
тогда окончательно запишем:
 Подставляя найденную величину в (2),
получим искомую формулу:
Подставляя найденную величину в (2),
получим искомую формулу:
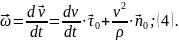 Таким
образом, проекции вектора
Таким
образом, проекции вектора
 на оси естественного трехгранника
равны:
на оси естественного трехгранника
равны:
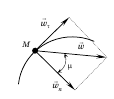
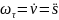 ,
,
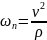 ,
,
 (5).
Вектор
(5).
Вектор
 будем называть
тангенциальной
или касательной
составляющей вектора
ускорения точки, а вектор
будем называть
тангенциальной
или касательной
составляющей вектора
ускорения точки, а вектор
 – его нормальной
составляющей. Модуль ускорения (рисунок)
точки M будет равен:
– его нормальной
составляющей. Модуль ускорения (рисунок)
точки M будет равен:
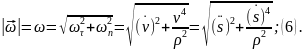
 Угол
μ между вектором
и главной нормалью
определяется из уравнения:
Угол
μ между вектором
и главной нормалью
определяется из уравнения:
 (7). Из
равенства (4) следует, что вектор
лежит в соприкасающейся плоскости
и направлен в сторону вогнутости
траектории. Пользуясь формулами
(5)–(6) можно определить модуль и
направление ускорения, если движение
задано естественным способом, т.е.
если известна траектория и задан
закон движения точки вдоль этой
траектории в виде:
(7). Из
равенства (4) следует, что вектор
лежит в соприкасающейся плоскости
и направлен в сторону вогнутости
траектории. Пользуясь формулами
(5)–(6) можно определить модуль и
направление ускорения, если движение
задано естественным способом, т.е.
если известна траектория и задан
закон движения точки вдоль этой
траектории в виде:
 Вектор
при этом направляется в сторону
положительного отсчета расстояния s
.
Криволинейное движение называется
ускоренным,
если проекции векторов
и
на ось
имеют одинаковые знаки и замедленным,
когда эти знаки разные. Если в данный
момент времени
Вектор
при этом направляется в сторону
положительного отсчета расстояния s
.
Криволинейное движение называется
ускоренным,
если проекции векторов
и
на ось
имеют одинаковые знаки и замедленным,
когда эти знаки разные. Если в данный
момент времени
 ,
(что может иметь место, когда |
| достигает максимума или минимума),
то
,
(что может иметь место, когда |
| достигает максимума или минимума),
то
 и
μ = 0 – ускорение в этот момент времени
направлено по главной нормали
и
μ = 0 – ускорение в этот момент времени
направлено по главной нормали
 Если же
в течение некоторого промежутка
времени, то на этом интервале времени
величина скорости
Если же
в течение некоторого промежутка
времени, то на этом интервале времени
величина скорости
 постоянна (равномерное
криволинейное движение),
а ускорение, появляющееся за счет
изменения вектора
по направлению, направлено вдоль
главной нормали
к траектории,
т.е
постоянна (равномерное
криволинейное движение),
а ускорение, появляющееся за счет
изменения вектора
по направлению, направлено вдоль
главной нормали
к траектории,
т.е
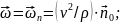 Аналогично, если в данный
момент времени
Аналогично, если в данный
момент времени
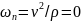 ,
то вектор
в этот момент направлен по касательной
к траектории
,
то вектор
в этот момент направлен по касательной
к траектории
 и μ = 90o
. Такой случай может иметь место, когда
в данный момент времени скорость
точки обращается в нуль (т.е. точка
меняет направление движения), или же
когда движущаяся точка находится в
точке перегиба своей траектории, где
ρ = ∞ . Если
же
и μ = 90o
. Такой случай может иметь место, когда
в данный момент времени скорость
точки обращается в нуль (т.е. точка
меняет направление движения), или же
когда движущаяся точка находится в
точке перегиба своей траектории, где
ρ = ∞ . Если
же
 в течение некоторого промежутка
времени, а точка движется
в течение некоторого промежутка
времени, а точка движется
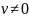 , то это может быть лишь в случае,
когда в течение всего промежутка
времени движение прямолинейно ρ = ∞ .
Если во все время движения численная
величина скорости постоянна, т.е.
, то это может быть лишь в случае,
когда в течение всего промежутка
времени движение прямолинейно ρ = ∞ .
Если во все время движения численная
величина скорости постоянна, т.е.
 , то криволинейное движение называется
равномерным.
Интегрируя равенство
, то криволинейное движение называется
равномерным.
Интегрируя равенство
 , найдем закон равномерного криволинейного
движения:
, найдем закон равномерного криволинейного
движения:
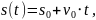 (8).
где
(8).
где
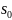 – расстояние от точки M до начала
отсчета
– расстояние от точки M до начала
отсчета
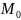 , вычисленное вдоль дуги траектории,
в начальный момент времени t = 0 . Если
касательное ускорение точки во все
время движения постоянно, т.е.
, вычисленное вдоль дуги траектории,
в начальный момент времени t = 0 . Если
касательное ускорение точки во все
время движения постоянно, т.е.
 ,
то криволинейное движение называется
равнопеременным.
Интегрируя равенство
,
то криволинейное движение называется
равнопеременным.
Интегрируя равенство
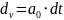 , найдем сначала закон скорости в этом
движении
, найдем сначала закон скорости в этом
движении
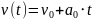 ;
(9) где
;
(9) где
 – начальная скорость точки. Принимая
во внимание, что
– начальная скорость точки. Принимая
во внимание, что
 , и интегрируя равенство (9), получим
закон равнопеременного криволинейного
движения в виде
, и интегрируя равенство (9), получим
закон равнопеременного криволинейного
движения в виде

