
- •1. Способы задания движения точки.
- •2. Определение скорости точки при задании ее движения векторным способом
- •3. Определение скорости точки при задании ее естественным способом.
- •4. Проекция на касательную к траектории.
- •5. Определение точки при задании ее координатным способом
- •6. Проекции скорости точки на неподвижные оси декартовых координат
- •7. Годограф скорости точки и его уравнения.
- •8. Прямолинейное движение, скорость и ускорение
- •9. Графическое представление закона движения точки.
- •10. Уравнения движения точки в декартовых координатах
- •11. Гармонические колебания.
- •12. Разложение скорости
- •13. Скорость в круговом движении. Угловая скорость
- •14. Закон равномерного, равнопеременного криволинейного движения
- •15. Секторная скорость.
- •16. Выражение скорости в криволинейных координатах.
- •18. Кривизна кривой. Радиус кривизны.
- •19.Проекции скоростей в ортогональной криволинейной системе координат.
- •20. Ускорение точки в криволинейной системе координат.
- •21 Скорость и ускорение точки в цилиндрической системе координат
- •22. Скорость и ускорение в сферической системе координат
- •23. Определение скорости точки в полярной системе координат
- •24. Поступательное движение твердого тела.
- •25. Теорема о перемещении тела, имеющего одну неподвижную точку. Угловая скорость тела.
- •26. Угловая скорость и угловое ускорение
- •27. Аксоиды мгновенных осей
- •28. Вращение вокруг неподвижной оси
- •29)Векторное выражение вращательной скорости и центростремительного ускорения.
- •30)Скорости и ускорения точек вращающегося тела.
- •31)Плоское движение твердого тела. Уравнения плоского движения.
- •32) Разложение плоского движения на поступательное движение вместе с полюсом и вращательное вокруг оси, проходящей через полюс.
- •33)Теорема об ускорении точек плоской фигуры и её следствие
- •34)План скоростей
- •36) Теорема о центре поворота для конечного перемещения плоской фигуры. Теорема Шаля
- •37)Теорема Эйлера-Даламбера:
- •38)Определение скоростей точек плоской фигуры с помощью мцс.
- •39)Мгновенный центр ускорений.
- •40)Векторные и скалярные формулы для скоростей и ускорений точек тела при его вращ.Вокруг неподвижной точки.
- •41) Свободное движение твердого тела. Скорости и ускорения его точек.
- •42) Относительное, переносное и абсолютное движение точки.
- •43) Сложное движение точки. Основные понятия и определения. Примеры.
- •44) Полная и относительная производная от вектора.
- •45. Сложное движение точки. Теорема о сложении скоростей.
- •49) Мгновенный центр ускорений.
- •50) Определение ускорений точек плоской фигуры
- •51) Сложение вращений вокруг двух параллельных осей
- •52) Основная теорема кинематики твердого тела (теорема о проекциях скоростей двух точек твердого тела на прямую, соединяющую эти точки).
- •53)В какой плоскости расположено ускорение точки и чему равны его проекции на естественные координатные оси?
- •54)Что характеризуют собой касательное и нормальное ускорение точки?
- •55)При каком движении точки равно нулю касательное ускорении и при каком нормальное?
- •56)Подвижные и неподвижные центроиды.
- •57. Напишите теорему Штейнера
- •58. Сложение мгновенных, угловых и поступательных скоростей.
- •59. Сложные поступательные движения.
- •60. Винтовое движение.
11. Гармонические колебания.
одним из часто встречающихся случаев в прямолинейном движении является гармоническое колебательное движение, закон которого дается уравнением:

Скорость точки при гармоническом колебании будет:
 ,
,
А
ускорение

Величина а есть наибольшее отклонение движущейся точки от начала отсчета О и называется амплитудой колебаний (рис.46) точка О называется центром колебаний, а промежуток времени, в течение которого точка возвращается в прежнее положение с той же скоростью – периодом колебаний.
![]()
Период определяется из условий:
 t+T)=
t+T)= и
и
 t,
t,
откуда
 .
.
Величина, обратная периоду, т.е.
 .
.
Называется
частотой
колебаний.
Аргумент синуса
 называется фазой
колебаний.
Величина
называется фазой
колебаний.
Величина
 называется
циклической
или круговой
частотой колебаний.
Кривой расстояний этого движения
является синусоида, кривой скоростей
– косинусоида, а кривой ускорений –
также синусоида, но сдвинутая по фазе
относительно графика движения на
называется
циклической
или круговой
частотой колебаний.
Кривой расстояний этого движения
является синусоида, кривой скоростей
– косинусоида, а кривой ускорений –
также синусоида, но сдвинутая по фазе
относительно графика движения на
 Как видно ускорение гармонического
движения точки пропорционально ее
отклонению от центра колебаний.
Как видно ускорение гармонического
движения точки пропорционально ее
отклонению от центра колебаний.
В
общем случае закон гармонических
колебаний дается уравнением
 ,
где величина
,
где величина
 является
начальной фазой колебаний. В частности,
при
является
начальной фазой колебаний. В частности,
при
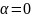 получаем закон: при
получаем закон: при
 закон движения будет
закон движения будет
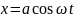 .
.
12. Разложение скорости
Представим радиус-вектор r точки в виде
r=rr0. (1)
Где r0 где единичный вектор по направлению r. При движении точки вектор r меняется по длине и по направлению, а следовательно, r0 и r суть некоторые функции времени. Дифференцируя равенство (1) по t, получим следующее выражение скорости точки:
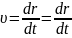 r0+
r0+ .
(2)
.
(2)
Скорость,
как видно из этого выражения, состоит
из двух слагаемых. Первое из них
 r0
имеет то же
направление, что и радиус-вектор r,
и характеризует изменение r
по модулю.
Чтобы выяснить смысл второго слагаемого,
заметим, что
r0
имеет то же
направление, что и радиус-вектор r,
и характеризует изменение r
по модулю.
Чтобы выяснить смысл второго слагаемого,
заметим, что
 ,
где
,
где
 - угол поворота вектора
- угол поворота вектора
 ;
следовательно, модуль второго слагаемого
будет:
;
следовательно, модуль второго слагаемого
будет:
 .
(3)
.
(3)
Направление
этого слагаемого перпендикулярно к
направлению
 ,
так как направление дифференциала
единичного вектора перпендикулярно к
направлению самого вектора. Тогда
,
так как направление дифференциала
единичного вектора перпендикулярно к
направлению самого вектора. Тогда
 ,
(4)
,
(4)
где
 есть единичный вектор направления,
перпендикулярного к r1.
Таким образом, второе слагаемое
представляет изменение вектора r
по направлению.
Окончательное выражение скорости
будет:
есть единичный вектор направления,
перпендикулярного к r1.
Таким образом, второе слагаемое
представляет изменение вектора r
по направлению.
Окончательное выражение скорости
будет:
 .
(5)
.
(5)
Первое
слагаемое
 называется радиальной
составляющей,
а второе слагаемое
называется радиальной
составляющей,
а второе слагаемое
 – трансверсальной(или
поперечной) составляющей скорости.
– трансверсальной(или
поперечной) составляющей скорости.
13. Скорость в круговом движении. Угловая скорость
Рассмотрим движение точки M по окружности радиуса R(рис 1). Скорость точки M в этом случае будет иметь численное значение

 ,
так как
ds=Rd
.
Величина
,
так как
ds=Rd
.
Величина
 называется угловой
скоростью вращения
радиуса OM
= R.
называется угловой
скоростью вращения
радиуса OM
= R.
Таким образом, при круговом движении скорость точки будет:
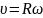 .
.
Направлена скорость по касательной к окружности, т.е. перпендикулярно к радиусу OM.
