
- •1. Способы задания движения точки.
- •2. Определение скорости точки при задании ее движения векторным способом
- •3. Определение скорости точки при задании ее естественным способом.
- •4. Проекция на касательную к траектории.
- •5. Определение точки при задании ее координатным способом
- •6. Проекции скорости точки на неподвижные оси декартовых координат
- •7. Годограф скорости точки и его уравнения.
- •8. Прямолинейное движение, скорость и ускорение
- •9. Графическое представление закона движения точки.
- •10. Уравнения движения точки в декартовых координатах
- •11. Гармонические колебания.
- •12. Разложение скорости
- •13. Скорость в круговом движении. Угловая скорость
- •14. Закон равномерного, равнопеременного криволинейного движения
- •15. Секторная скорость.
- •16. Выражение скорости в криволинейных координатах.
- •18. Кривизна кривой. Радиус кривизны.
- •19.Проекции скоростей в ортогональной криволинейной системе координат.
- •20. Ускорение точки в криволинейной системе координат.
- •21 Скорость и ускорение точки в цилиндрической системе координат
- •22. Скорость и ускорение в сферической системе координат
- •23. Определение скорости точки в полярной системе координат
- •24. Поступательное движение твердого тела.
- •25. Теорема о перемещении тела, имеющего одну неподвижную точку. Угловая скорость тела.
- •26. Угловая скорость и угловое ускорение
- •27. Аксоиды мгновенных осей
- •28. Вращение вокруг неподвижной оси
- •29)Векторное выражение вращательной скорости и центростремительного ускорения.
- •30)Скорости и ускорения точек вращающегося тела.
- •31)Плоское движение твердого тела. Уравнения плоского движения.
- •32) Разложение плоского движения на поступательное движение вместе с полюсом и вращательное вокруг оси, проходящей через полюс.
- •33)Теорема об ускорении точек плоской фигуры и её следствие
- •34)План скоростей
- •36) Теорема о центре поворота для конечного перемещения плоской фигуры. Теорема Шаля
- •37)Теорема Эйлера-Даламбера:
- •38)Определение скоростей точек плоской фигуры с помощью мцс.
- •39)Мгновенный центр ускорений.
- •40)Векторные и скалярные формулы для скоростей и ускорений точек тела при его вращ.Вокруг неподвижной точки.
- •41) Свободное движение твердого тела. Скорости и ускорения его точек.
- •42) Относительное, переносное и абсолютное движение точки.
- •43) Сложное движение точки. Основные понятия и определения. Примеры.
- •44) Полная и относительная производная от вектора.
- •45. Сложное движение точки. Теорема о сложении скоростей.
- •49) Мгновенный центр ускорений.
- •50) Определение ускорений точек плоской фигуры
- •51) Сложение вращений вокруг двух параллельных осей
- •52) Основная теорема кинематики твердого тела (теорема о проекциях скоростей двух точек твердого тела на прямую, соединяющую эти точки).
- •53)В какой плоскости расположено ускорение точки и чему равны его проекции на естественные координатные оси?
- •54)Что характеризуют собой касательное и нормальное ускорение точки?
- •55)При каком движении точки равно нулю касательное ускорении и при каком нормальное?
- •56)Подвижные и неподвижные центроиды.
- •57. Напишите теорему Штейнера
- •58. Сложение мгновенных, угловых и поступательных скоростей.
- •59. Сложные поступательные движения.
- •60. Винтовое движение.
6. Проекции скорости точки на неподвижные оси декартовых координат
Направленные отрезки принято называто также геометрическими векторами или просто векторами. Вектор как направленный отрезок мы будем по-прежнему записывать в тексте двумя большими латинскими буквами с общей чертовй наверху при условии, что первая из них обозначает начало, вторая - конец вектора. Наряду с этим мы будем также обозначать вектор одной малой латинской буквой полужирного шрифта, которая на чертежах ставится у конца стрелки, изображающей вектор (рис. 1, где изображен вектор а с началом А и концом В). Начало вектора часто будет называться таже его точкой приложения.
![]()
Векторы называются равными, если они имеют одинаковые длины, лежат на параллельных прямых или на одной прямой и направлены в одну сторону.
Число,
равное длине вктора (при заданном
масштабе), называется его модулем.
Модуль вектора a обозначается
символом ![]() или
а. Если
или
а. Если ![]() ,
то вектор
,
то вектор ![]() называется
единичным.
называется
единичным.
Единичный
вектор, имеющий одинаковое направление
с данным вектором
,
называется ортом вектора
и
обозначается обычно символом ![]() .Проекцией
вектора
.Проекцией
вектора ![]() на
ось u называется
число, равное величине отрезка
на
ось u называется
число, равное величине отрезка ![]() оси u,
где точка
оси u,
где точка ![]() является
проекцией точки А на ось u,
а
является
проекцией точки А на ось u,
а ![]() -
проекцией точки В на эту ось.
-
проекцией точки В на эту ось.
Проекция
вектора
на
ось u обозначается
символом ![]() .
Если вектор обозначен символом
,
то его проекцию на ось u принято
обозначать:
.
Если вектор обозначен символом
,
то его проекцию на ось u принято
обозначать: ![]() .
.
Проекция
вектора
на
ось u выражается
через его модуль и угол ![]() наклона
к оси u формулой
наклона
к оси u формулой
![]() .
.
Проекции
произвольного вектора
на
оси некоторой заданной системы координат
в дальнейшем обозначаются буквами X,
Y, Z. Равенство
={X,
Y, Z} означает, что числа X,
Y, Z являются
проекциями вектора на координатные
оси. Вектор, для которого X=Y=Z=0,
называется нулевым и обозначается ![]() .
.
Проекции
вектора на координатные оси называются
также его (декартовыми) координатами.
Если даны две точки ![]() (
(![]() ,
, ![]() ,
, ![]() )
и
)
и ![]() (
(![]() ,
, ![]() ,
, ![]() ),
являющиеся соответственно началом и
концом вектора
,
то его координаты X,
Y, Z определяются
по формулам
),
являющиеся соответственно началом и
концом вектора
,
то его координаты X,
Y, Z определяются
по формулам ![]() ,
, ![]() ,
, ![]() .
.
Формула
![]() (2)
(2)
позволяет по координатам вектора определить его модуль.
Если ![]() ,
, ![]() ,
, ![]() -
углы, которые составляет вектор
с
координатными осями (см. рис. 2),
то
-
углы, которые составляет вектор
с
координатными осями (см. рис. 2),
то ![]() ,
, ![]() ,
, ![]() называются
направляющими косинусами вектора
.
называются
направляющими косинусами вектора
.

Вследствие формулы (1)
![]() ,
, ![]() ,
, ![]() .
.
Отсюда, и из формулы (2) следует, что
![]() .
.
Последнее равенство позволяет определить один из углов , , , если известны два других.
7. Годограф скорости точки и его уравнения.
Годограф
(Hodograph) — скорость движущейся точки есть векториальная величина (см. Вектор), изображаемая длиною, откладываемою от положения движущейся точки по направлению движения и заключающею в себе столько единиц длины и частей ее, сколько в изображаемой скорости заключается единиц скорости и частей ее. Чтобы составить наглядное представление об изменении величины и направления скорости при каком-либо криволинейном движении точки, Гамильтон (см.) предложил строить вспомогательную кривую, названную им Г. скорости; эта кривая образуется оконечностями векторов, изображающих скорости, отложенных от одной и той же неподвижной точки, напр. от начала координат.
Возьмем, напр., движение тяжелой материальной точки в среде, сопротивление которой движению пропорционально скорости. Это движение выражается уравнениями:
x = (a/k)(1 — f)
y = -(g/k)t + (1/k)(ß + g/k)(1 — f)
где f = е-kt, а и ß — проекции начальной скорости vo на оси Х и У, g — ускорение силы тяжести, действующей по направлению отрицательной оси У, k — коэффициент сопротивления среды. На прилагаемом чертеже изображены: траектория движущейся точки и Г. скорости.
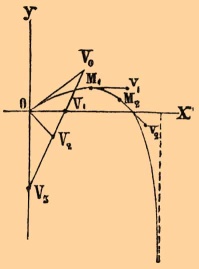
Траектория, начинаясь в точке О, имеет наивысшую точку в M1, где скорость параллельна оси Х; затем, опускаясь к оси Х, она наконец пересекает эту ось и после того асимптотически приближается к означенной прерывною чертою прямой, параллельной отрицательной оси У. Г. скорости есть прямая VoV3, начинающаяся в точке Vo — конце вектора OVo, изображающего начальную скорость vo, и кончающаяся в точкеV3 — конце вектора OV3, изображающего скорость g/k, к которой приближается скорость движущейся точки по мере возрастания t до бесконечности. По мере того, как движущаяся точка описывает траекторию, точка, описывающая Г., непрерывно перемещается от Vo к V3. Радиус вектор OV1 изображает скорость v1 в наивысшей точке траектории, радиус вектор OV2 — скорость в точке М2, где касательная параллельна OV2 и т. д.
Скорость точки, описывающей Г., определяет величину и направление ускорения движущейся точки (см. Ускорение). Способ построения Г. применяется в механике для различных целей и к другим непрерывно изменяющимся с течением времени векториальным величинам. Таковы Г. угловой скорости, главного момента количеств движений и проч.
