1. Способы задания движения точки.

Определить движ. точки- значит определить ее положение относительно выбранной системы отсчета в любой момент времени. Это делается одним из следующих способов.

А) Естественный способ определения движения точки требует задания ее траектории относительно выбранной системы отсчета xyz (рис.36).

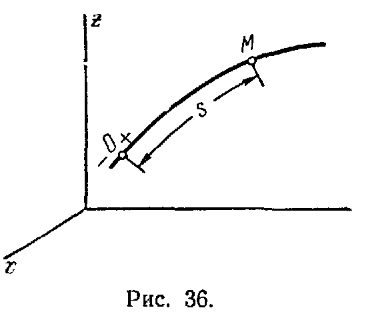
на траектории следует задать начало и положительное направление отсчета расстояний s=OM; расстояние s от начала отсчета О до точки М, измеренное вдоль дуги траектории и взятое с соответствующим знаком, будет однозначно определять положение точки М на траектории, а следовательно и в системе отсчета xyz. Далее должно быть указано начало отсчета времени (начальный момент t=0). Тогда движение точки будет определено, если для каждого момента времени t будет известна величина s, указывающая положение точки, т.е. если будет дана зависимость s=f(t) (1). Равенство (1) это закон движение точки.

При естественном способе опред-ния движ-ия точки должны быть заданы

Траектория точки

Начало отсчета расстояний на траект-ии с указанием положительного направления отсчета и начальный момент времени

Закон движения точки вдоль траектории в виде s=f(t)

По самой природе движение функция f(t) должна быть:

Однозначной, ибо в один и тот же момент времени движущаяся точка не может находиться в двух различных точках пространства;

Непрерывной, ибо движение непрерывно и поэтому каждому бесконечно малому изменению t соответствует бесконечно малое изменение s.

Дифференцируемой , т.е. должна пропускать производную.

Если s=c=const, то это означает, что точка относительно данной системе отсчета находится в покое

Б) Координатный способ определение движение точки состоит в том ,что даются: 1) какая- либо система координат (система ориентировки), связанная с телом отсчета, и 2) координаты движущейся точки, как функция времени.

Положение точки в пространстве трех измерений определяется тремя числами , которые называются криволинейными координатами точки. Следовательно, закон движение точки будет в общем случае задаваться уравнениями (2). Чаще всего для определения положения точки используется прямоугольная декартовая система координат xyz. В этой системе координат движение точки задается в виде x=x(t), y=y(t), z=z(t) (3). Каждое из трех уравнений (3), взятое отдельно, определяет закон движения проекции точки на соответствующую ось; считают, что при этом способе задания исследуемое движение разлагается по направлениям осей координат и представляется как совокупность 3-х движений вдоль этих взаимно перпендикулярных осей.

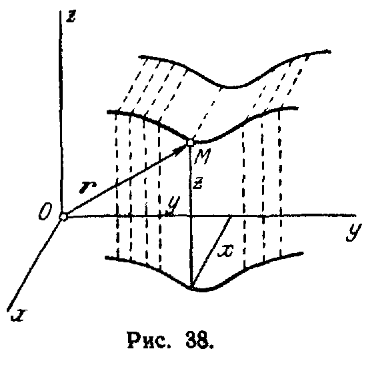
В) Векторный способ определения движение точки основан на задании ее положение радиусом- вектором r, проведенным из начала О выбранной системы ориентировки (см. рис. 38). Так как r=xi+yj+zk ,то в векторной форме закон движение точки представится в виде r=r(t)=x(t)i+y(t)j+z(t)k (5)

Траекторией точки при векторном задании движения будет годограф радиус вектора r (см. рис. 38).

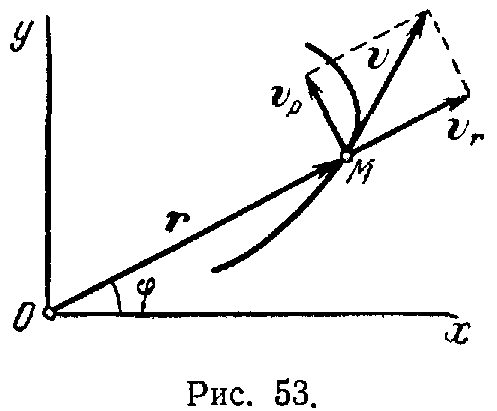
В случае плоского движения, т. е. когда траектория есть плоская кривая, закон движения точки относительно какой-либо системы координат, расположенной в плоскости движения, выразится только двумя уравнениями. В частности, в случае плоской декартовой системы координат (ху) будем иметь: x=x(t), y=y(t) (6), а в случае плоской полярной системы координат (r, ) (см. рис. 53)

r=r(t), (7) где r — полярный радиус.

Векторное выражение закона плоского движения будет; r=r(t)=x(t)i+y(t)j (8)

где г — полярный радиус.

Исключая t в системах (6) или (7), получим уравнения траектории плоского движения в декартовых координатах: f(x,y)=0, или в полярных Ф(r , )=0. По характеру траектории движение точки может быть прямолинейным и криволинейным, причем эти свойства траектории ,конечно , зависят от выбора системы отсчета. Движение, прямолинейное относительно одной системы отсчета, может быть криволинейным относительно другой, и наоборот.