Теоремы о дифференцируемых функциях.

1. Теорема Ферма. Если ф-ия y=f(x) определена и непрерывна на отрезке [a,b] и достигает наибольшего или наименьшего значения в некоторой точке x_o из интервала (a,b), то, если она в этой точке имеет конечную производную, то f´(x₀)=0.

2. Теорема Роля. Если ф-ия y=f(x) определена и непрерывна на отрезке [a,b], дифференцируема на интервале (a,b) и f(a)=f(b), то на интервале (a,b) существует по крайней мере одна т. ξ, такая, что f´(ξ)=0. С геомерич. точки зрения данная теорема означает, что при выполнении условий теоремы существует по крайней мере одна точка на интервале, в кот. касательная параллельна абсцисс.

3. 

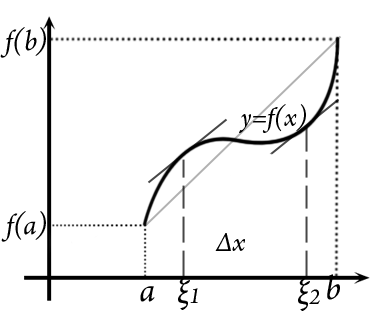
Теорема Лагранжа.Пусть ф-ия y=f(x) определена и непрер. на на отрезке [a,b] и дифференцируема на интервале (a,b),тогда на интервале (a,b) существует по крайней мере одна т. ξ, такая, что .

4. Теорема Коши. Пусть даны 2 ф-ии f(x) и g(x), определенные и непрерывные на отрезке [a,b] и дифференцируемые на интервале (a,b), причем для любого x из интервала (a,b) g´(x)≠0, тогда на интервале (a,b) существует по крайней мере одна т. ξ, такая, что .

Правило Лопиталя.

Рассмотрим задачу раскрытия неопределенности отношения двух ф-ий f(x) и g(x), когда ф-ии f(x) и g(x) определенны и непрерывны на отрезке [a,b] ,дифференцируемые на интервале (a,b) и при x→x₀ явл. одновременно БМФ или ББФ, тогда предел отношения этих ф-й=пределу отношения производных этих ф-ий.

Замечание. Правилом Лопиталя можно пользоваться только в случае раскрытия неопределенности 0/0 или ∞/∞. При остальных неопр-тях прежде всего необходимо перейти к этим неопр-тям, а потом использовать правило Лопиталя.

А симптоты

Определенный интеграл.

Рассм. задачу: пусть на некотором отрезке [а;в] задана непрерывная ф-ия, принимающая во всех точках этого отрезка неотрицательные значения ∀x∈[а;в], f(x)≥0, рассм. фигуру, огранич. y=f(x)

РИСУНОК

Задача состоит в нахождении площади данной трапеции. Разобьем отрезок [а;в] на n-частей и через точки разбиения проведем вертикальные прямые, получим n-криволинейных трапеций. В каждой такой трапеции найдем минимальные значения ф-ии mi и максимальные значения ф-ии Mi.

Построим в каждой трапеции прямоугольник с высотой mi и Mi и определим площади этих прямоугольников: mi × ∆xi и Mi × ∆xi, где xi=(b-a)/n. Сложив площади этих прямоугольников, получим: . Первая из этих сумм называется нижняя сумма Дарбу, а вторая — верхняя сумма Дарбу. Нижняя сумма определяет площадь криволинейной трапеции с недостатком, а верхняя — с избытком, т. е. площадь трапеции, если ее рассм. как последовательность в зависимости от n(Sn) удовлетворяет неравенству: . В этом неравенстве перейдем к пределу при n→∞, обозначим , , получим неравенство: , т.е. . Дарбу показал, что при n→∞,, последовательности верхних и нижних сумм Дарбу стремятся к одной и той же велечине, по теореме о переходе к пределу в неравенствах (теорема о 3 милиционерах), lim Sn также равен этой величине, которая по сути дела и определяет площадь заданной трапеции. РИС 2 Этот предел назвали определенным интегралом.

Определенным интегралом от ф-ии f(x) на отрезке [а;в] называют конечный предел интегральной суммы, при n→∞. , где mi≤(ξi)≤Mi.

Теорема 1(об интегрируемых ф-ях). Если ф-ия y=f(x) определена и непрерывна на отр. [а;в] всюду за исключением конечного числа точек разрыва 1 рода, то она интегрируема на этом отрезке, т.е. имеет конечный предел интегральной суммы.

Теорема 2(об интегрируемых ф-ях). Если ф-ия y=f(x) определена и является монотонной на отр. [а;в], то она интегрируема на этом отрезке.

Свойства (определ. интеграла):

1. Если ф-ия y=f(x) интегрируема на отр. [а;в], то ф-ия kf(x) также интегрируема на отр. [а;в].

2. Если ф-ии f₁(x) и f₂(x) интегрируемы на отр. [а;в], то ф-ии f₁(x)±f₂(x) также интегрируемы на этом отр. и выполняются формулы:

3.

4.

5. Св-ва аддитивности опред. интеграла:

, где a<c₁<c_n<b.

Геометрический смысл св-ва аддитивности: S=S1+S2+S3

РИСУНОК3

6. Пусть ф-ия y=f(x) интегрируема на отр. [а;в] и f(x)≥0, ∀x∈[а;в], тогда

7. Пусть ф-ии f(x) и g(x) интегрируемы на отр. [а;в] и∀x∈[а;в], выполняется неравенство: f(x)≥g(x), то

8. Пусть ф-ия y=f(x) интегрируема на отр. [а;в] и a<b, тогда ф-ия y=|f(x)| также интегрируема на этом отрезке, причем .

9. Пусть функция y=f(x) интегрируема на отрезке [а;в] и на этом отрезке ф-ия принимает значение, удовлетворяющее неравенству ,тогда справедливо неравенство

10.Если функция y=f(x) интегрируема на отрезке ab и непрерывна, то на этом отрезке существует некоторая точка .. такая что

11.Если функция y=f(x) непрерывна и нечетна на отрезке ab, то

12. Если функция y=f(x) непрерывна и является четной, то

Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.

Пусть функция y=f(x)интегрируема на (ab), рассмотрим некоторую точку x из интервала (ab), отрезок (a;x) (a;b)

Функция называется интегралом с переменным верхним пределом

Свойства интеграла:

1.Если функция f(x) интегрируема на отрезке ab, то функция непрерывна в любой точке этого отрезка.

2.Если функция f(x) непрерывна в точке x0, то функция имеет производную в точке x0 и выполняется равенство Из этого свойства очевидно, что F(x) есть первообразная для функции f(x).

3. Если функция F(x) есть первообразная для функции f(x) и она непрерывна на отрезке ab, то

-Формула Ньютона-Лейбница.

Приложения определенного интеграла.

1.Площади плоских фигур.

Пусть функция y=f(x) непрерывна на отрезке ab и принимает на нем неотрицательное значение тогда площадь криволинейной трапеции S

2. Пусть функция y=f(x) непрерывна на отрезке ab и

3.Пусть на отрезке ab заданы две непрерывные функции f(x) и g(x) причем

Чтобы найти площадь ограниченную графиком этих функций прежде всего необходимо определить абсциссы точек из пересечения f(x)=g(x). Предположим, что это x1 и x2 тогда

2. Вычисления объемов тела по известной площади поперечного сечения .

Пусть задано некоторое тело и предположим, что известна площадь сечения, которая проводится перпендикулярно оси Ox. Эта площадь проводится определяется обычно точкой x и представляет собой функцию тогда объем данного тела есть

3.Объем и тело вращения.

Рассмотрим тело, которое образовано вращением вокруг оси Ox криволинейной трапеции, ограниченной y=g(y) 0, y=0, x=a, x=b.

Объем этого тела

Если криволинейная трапеция, ограниченная x=g(y) , y=a, y=b, x=0, вращается вокруг оси Oy, то объем полученного тела вычисляется по формуле