82.Числовые характеристики двумерной случайной величины:

математическим ожиданием составляющей  двумерной дискретной случайной величины  называют число:

Математическим ожиданием составляющей   двумерной дискретной случайной величины  называют число:

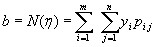
математическим ожиданием составляющей   непрерывной двумерной случайной величины  называют число:

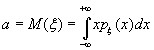, где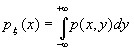 

В результате получим:

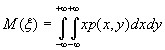
Математическим ожиданием составляющей   непрерывной двумерной случайной величины  называют число:

дисперсией составляющей   двумерной дискретной случайной величины называют число:

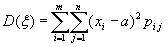
Дисперсией составляющей   двумерной дискретной случайной величины называют число:

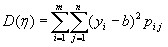
дисперсией составляющей   двумерной непрерывной случайной величины  называют число:

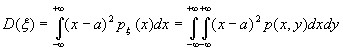
дисперсией составляющей   двумерной непрерывной случайной величины  называют число:

Корни квадратные из дисперсии называют средними квадратичными отклонениями составляющих:

Ковариацию вычисляют по формулам cov(x , h )=M[(x - Mx )(h - Mh )] = M(x h) - Mx Mh .

Если случайные величины x и h независимы, то cov(x ,h )=0.

Ковариационной матрицей случайного вектора (x ,h ) называется матрица вида

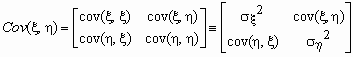
 безразмерный коэффициент корреляции  .

Корреляционной матрицей случайного вектора называется матрица

.

83.Условия независимости случайных величин:

Теорема. Для того, чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы функция распределения системы (X, Y) была равна произведению функций распределения составляющих.

Аналогичную теорему можно сформулировать и для плотности распределения: Теорема. Для того, чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы плотность совместного  распределения системы (X, Y) была равна произведению плотностей распределения составляющих.

84 Коэффициент корреляции св и его свойства.

Коэффициент корреляции — это мера взаимосвязи измеренных явлений.

Пусть — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:

Свойства:

1. 

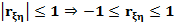
2. Коэффициент корреляции равен тогда и только тогда, когда линейно зависимы:

3. Если независимые СВ ,то

85.Понятие о законе больших чисел. Теорема Бернулли

Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел.

Закон больших чисел - это обобщенное название нескольких теорем, из которых следует, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным. К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли - простейшим.

Теорема Бернулли

Если в каждом из n независимых испытаний вероятность появления события A постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико. Другими словами, если сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство

При доказательстве теоремы Бернулли получаем оценку

p