4.Понятие дифференцируемости ф-ции двух переменных. Полный диффер.
Пусть
ф-ция z=f(x;y)
определена в некоторой окрестн. т.
M(x;y).
Составим полное приращение ф-ции в т.:
М 
z=f(x+
;
y+
y)-f(x;y).
Ф-ция z=f(x;y)
назыв. дифференцируемой
в
т. M(x;y),
если ее полное приращение в этой т. можно
представить в виде 
A
x+B·
·
x+
,
где 
→0
и 
(
x;
y)
при
x→0,
y→0.
Сумма первых двух слагаемых в равенстве
представляют собой главную
часть приращения ф-ции. Гл.
часть приращения ф-ции z=f(x;y),
линейная относительно 
,
назыв. полным
дифференциалом
этой ф-ции и обознач. dz:
dz=A·
.
Выражен. A·
назыв. частными
дифференциалами.
Если ф-ция z= f(x;y) дифференцируема в т.
М(х;у) то она непрерывна в этой точке,
имеет в ней частные производные
и
, причем
=A
,
=B.
Если ф-ция z=f(x;y)
имеет непрерывные частные производные
и 
в т. М(х;у) то она дифференцируема в этой
т. и ее полный дифференциал выражается
ф-лой dz=
dx+
dy
или dz=
.
5.Производная по направлению. Градиент .
.Производной
от ф-ции
V — U(M)
в
т.М
по
направлению λ назыв. предел 
=
=
.
Переходя к пределу при 
0,
получим ф-лу для вычисления производной
по направлению: 
=
+
+
.
Вектор, координатами которого яв-тся
значен. частных производных ф-ции
U{x;y;z)
в т.M(x;y;z), назыв. градиентом ф-ции и
обозначают grad U,
т. е. grad U = (
;
;
),
или grad U = (
;
;
).
Приведем важные св-ва градиента ф-ции.
1. Градиент направлен по нормали к поверхности уровня, проходящей через данную точку.
2. grad(U+V) = gradU+ gradV, 3.grad(c · U) - с·gradU, с = const,
4.grad(U•
V) = U grad V + V grad U, 5.grad(
)=
, 6.gradF(U)=
gradU.
6. Поверхности уровня. Уравнение касательной плоскости к поверхности.
Определение. Касательной плоскостью к поверхности в данной точке касания называется плоскость, в которой лежат касательные в этой точке к всевозможным кривым, проведенным на данной поверхности через указанную точку.
Поверхностью уровня скалярного поля u = u(x,y,z)называется множество точек пространства, в которых функция u принимает одно и то же значение c, то есть поверхность уровня определяется уравнением u(x,y,z) = c.
7. Касательная плоскость и нормаль к поверхности
Плоскость альфа -касательная плоскость к поверхности S в точке M.
8 . Экстремумы функций двух переменных.
9. Нахождение наибольшего и наименьшего значений на компакте. Понятие об условном экстремуме.
Условные
экстремумы.
Пусть функция 
определена
в некоторой области 
и
в этой области задана кривая уравнением 
.
Условным экстремумом функции двух
переменных
называют
ее экстремум при условии, что точки
берутся на заданной кривой. Если из
уравнения кривой можно, например,
выразить 
,
то задача о нахождении условного
экстремума сводится к исследованию на
экстремум функции одной переменной 
.
Определённый интеграл как предел интегральных сумм. Геометрически смысл ои.
С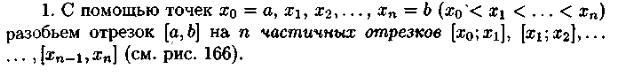
умма
11.Основные
св-ва интегралов(ОИ).
1)Постоянный
множитель можно вынести за знак ОИ:если
А=const,то
2)ОИ
от алгебраической суммы нескольких
ф-ций равен алгебраич.сумме интегралов
от слагаемых: 
.
3)Если
на отрезке [a,b],где
а<b,ф-ции
f(x)
φ(x)
удовлетворяют условию f(x)<=φ(x),то
.
4)Если
m
и М-наименьшее и наибольшее значения
ф-ции f(x)
на отрезке [a,b]
и а <=b,
то: m(b-a)<=
.
5)(Теорема
о среднем). Если ф-ция f(x)
непрерывна на отрезке [a,b],
то на этом отрезке найдется такая точка
£,что справедливо след.равенство: 
.
6)Для
любых трех чисел a,b,c
справедливо равенство: 
,
если только все эти три интеграла
существуют.
7)
;
.