
- •01.Предмет, задачи и анализ статистики.
- •2.Статистическое наблюдение(программно-методологические и организационные вопросы).
- •3.Формы,видыспособы статистического наблюдения.
- •4.Сущность выборочного метода.Генеральная и выборочная совокупности.
- •5.Виды отбора единиц в выборочную совокупность.
- •6 Ошибки выборочного наблюдения, примеры.
- •7. Определение численности выборки, примеры.
- •8. Сводка и группировка статических данных
- •9. Этапы группировки. Ряды распределения, примеры.
- •10. Статистические таблицы и графики
- •12) Средние величины. Примеры
- •13) Структурные средние. Примеры
- •14) Показатели вариации. Примеры
- •15) Моменты распределения. Показатели асимметрии и …
- •21 Критерий Дурбина – Ватсона. Индекс сезонности.
- •25. Основные задачи индексного метода. Индивидуальный и сводные индексы.
- •26. Агрегатная форма сводных индексов. Сводные индексы в агрегатной форме цен, товарооборота, физического объема реализации. Примеры.
- •1) Сводный индекс товарооборота.
- •30. Территориальные индексы. Примеры.
- •31. Статистические методы изучения связи между двумя признаками. Расчет коэффициента корреляции.
- •32. Анализ связи двух порядковых переменных
- •33. Анализ связи двух номинальных переменных
- •34. Корреляционно-регрессионный анализ
- •17Методы исчисления показателей ряда динамики.
- •24. Критерии согласия. Критерий Пирсона, Критерий Романовского, Критерий Холмогорова.
- •19) Структура ряда динамики. Методы выделения тренда.
- •20) Аналитическое выравнивание ряда динамики.
- •23) Выравнивание вариационных рядов. Закон распределения Пуассона.
- •16. Динамические ряды и их виды. Пример
- •18. Средние характеристики ряда динамики. Пример
- •19. Структура ряда динамики. Методы выделения тренда. Метод скользящей средней.
20) Аналитическое выравнивание ряда динамики.
Метод аналитического выравнивания предполагает нахождение аналит., графической зависимости законом измен-я уровня ряда динамики во времени.
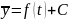 (дальше
будут все у от t).
(дальше
будут все у от t).
В качестве основных зависим-й выбираем:
Линейная зависимость. 2) Параболическая зависимость:
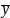 =
=
 .
3)Экспоненциальная
зависимость
.
3)Экспоненциальная
зависимость
 ;
;
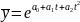 .
Рассмотрим
линейную зависимость: 1) а0;а1 находится
из (*). 2) а0, а1, а2 =?(для параболической
зависимости). Найдём их, исполняя метод
наим. кв.в.:
.
Рассмотрим
линейную зависимость: 1) а0;а1 находится
из (*). 2) а0, а1, а2 =?(для параболической
зависимости). Найдём их, исполняя метод
наим. кв.в.:
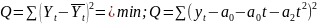 => min.
=> min.
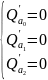 =>
=>
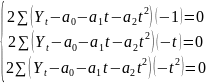 /:2
/:2
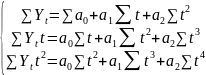
∑t=0;
∑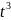 =0.
=0.
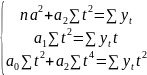
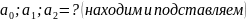
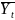 =
=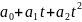 ;
;
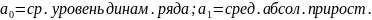
23) Выравнивание вариационных рядов. Закон распределения Пуассона.
(1) - Основной задачей анализа вариационных рядов является изучение законов распределения и выявление характера зависимости. В ходе анализа выдвигают гипотезу о близости рассматриваемого фактического распределения к 1-му из хорошо известных типов теоретических распределений. Под теоретическим распределением понимается графическая кривая, а также распределение в чистом.виде, где накл-ся влияние случайных факторов. Чаще всего исполняют нормал. распред., распред.Пуассона.
Нормальное распределение.
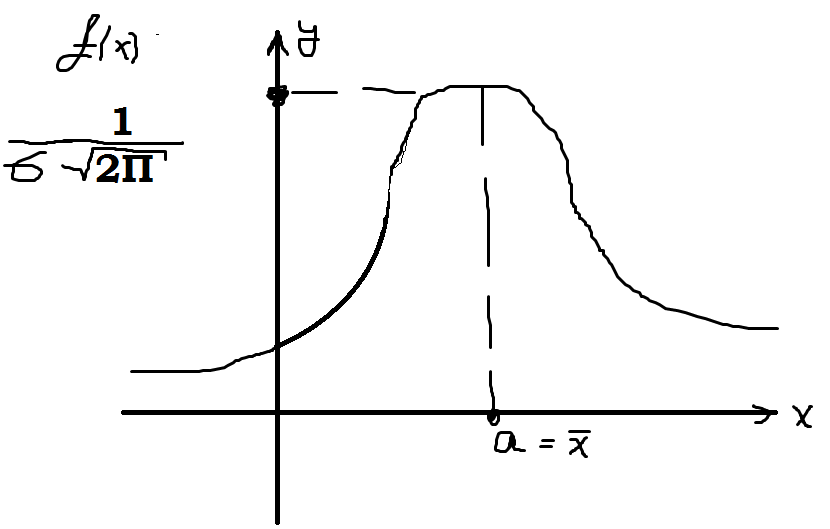
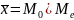
 – плотность
распределения вероятности.
– плотность
распределения вероятности.
 =t
– стандартизац-е отклонение(нормированное).
=t
– стандартизац-е отклонение(нормированное).
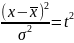 ;
;
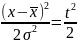 ;
;
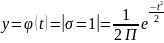 .
.

е, П – математическая постоянная.
(σ) – сред.квадр. отклонение.
- дисперсия
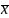 – сред.
арифм.(сред.величины).
– сред.
арифм.(сред.величины).
Свойства кривой нормального распределения.
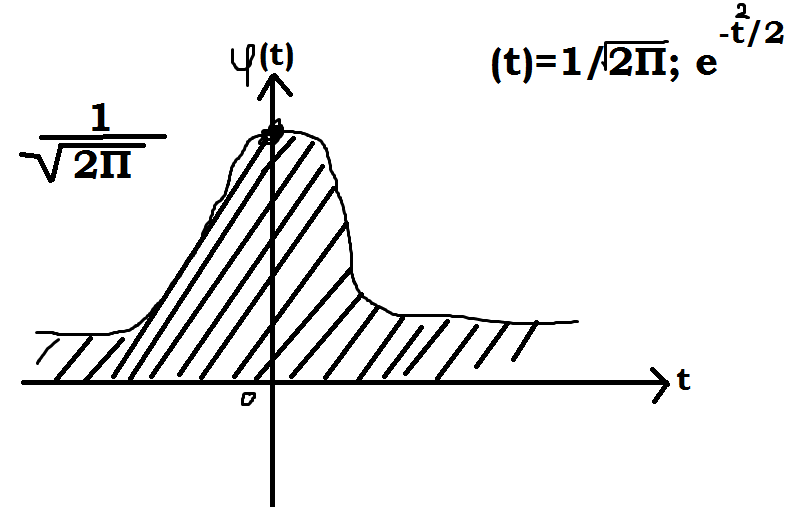
φ (-t)= φ (t)- функция четная.
φ (0)=
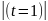 =
=
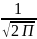 ;
;S=1.
t=>
 ;
φ (t)=>0;
;
φ (t)=>0;Можно найти точки перегиба
 0.
0.φ (t)= φ (t) – табул.значения.
При выравнивании вариационных рядов по кривой нормального распределения теоретические частоты вычисляются:
 2)
2)
 .
.
N
– общее число единиц.
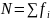 (частот); h
– длина интервалов в группах. (σ)
– сред.квадратич.отклон-е.
(частот); h
– длина интервалов в группах. (σ)
– сред.квадратич.отклон-е.
Сравниваем полученные теоритические частоты с дан. убеждаемся, что их расхождения не велики, но это сопоставление графика эмпирических данных частот с теоритическими позволяет оценить эти расхождения субъективно, объективно с помощью критерия Согласия.
 (получен.).
(получен.).
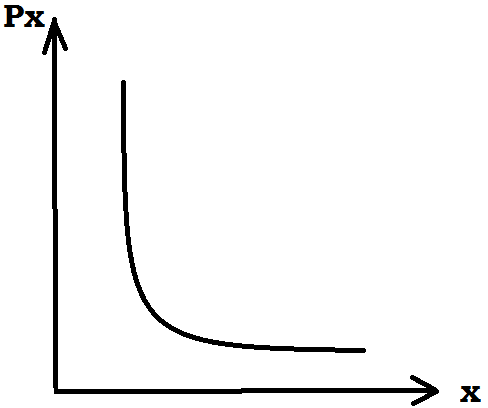
(2)
– В ряде случаев, если вариационный
ряд представляет собой распредел-е по
дискретному признаку, т.е. где по мере
увеличения значений признака
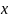 частоты резко уменьшаются, где
частоты резко уменьшаются, где
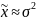 .
.
 .
.
 – вероятность наступления отдельных
значений
– вероятность наступления отдельных
значений


То такой ряд можно выровнять по кривой Пуассона. При выравнивании ряда по закону Пуассона теорем.частоты определяется по формуле:
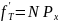 N-
общее число единиц ряда.
N-
общее число единиц ряда.Полученные теоретические частоты и данные фактические необходимо уравнять между собой и проверить, есть ли между ними различия, и если они есть, то случайные ли они или существ.? Таким образом проверяется гипотеза о характере распределения с помощью критерия Согласия.
16. Динамические ряды и их виды. Пример
Определение:
Рядом динамики наз-ся
последова-ть значений статистического
показателя признака, упорядоченная в
хронологическом порядке, т.е. в порядке
возрастания временного параметра.
Отдельные наблюдения врем-го ряда
наз-ся уровне ряда
 .
Каждый ряд динамики содержит два
элемента: 1)Значение времени; 2)Значение
уровня ряда. В зависимости от хар-ра
временного параметра ряды делятся на
моментные и интервальные. В
моментных рядах динамики
уровни характеризуют значение показателей
по состоянию на определенные моменты
времени(даты). Например, ряды цен на
определенные уровни товаров. Ряды
курсов акций, уровни которых фиксируются
в конкретных числах. Ряды численности
мужского и женского населения , ряды
стоимости основных производственных
фондов. Т.к. значение уровней этих рядов
опреде-ся ежегодно на одно и тоже число.
В
интервальных рядах
уровни характер-ся значениями показателя
за определенные интервалы. Например,
ряды годовой, месячной, квартальной,
динамики производства продукции в
натуральном или стоимостном выражении.
Уровне рядов динамики могут представлять
собой абсолютные, относительные и
средние величины. В таком случае ряды
наз-ся производными.
Правило построения рядов динамики:
1)необходимо соблюдать периодичность
развития явления.2)величины временных
интервалов должны соответствовать
интенсивности изменения изучаемого
объекта.3)числовые уровни рядов динамики
должны быть упорядочены во времени, не
допускается анализ рядов динамики с
пропуском во времени.
.
Каждый ряд динамики содержит два
элемента: 1)Значение времени; 2)Значение
уровня ряда. В зависимости от хар-ра
временного параметра ряды делятся на
моментные и интервальные. В
моментных рядах динамики
уровни характеризуют значение показателей
по состоянию на определенные моменты
времени(даты). Например, ряды цен на
определенные уровни товаров. Ряды
курсов акций, уровни которых фиксируются
в конкретных числах. Ряды численности
мужского и женского населения , ряды
стоимости основных производственных
фондов. Т.к. значение уровней этих рядов
опреде-ся ежегодно на одно и тоже число.
В
интервальных рядах
уровни характер-ся значениями показателя
за определенные интервалы. Например,
ряды годовой, месячной, квартальной,
динамики производства продукции в
натуральном или стоимостном выражении.
Уровне рядов динамики могут представлять
собой абсолютные, относительные и
средние величины. В таком случае ряды
наз-ся производными.
Правило построения рядов динамики:
1)необходимо соблюдать периодичность
развития явления.2)величины временных
интервалов должны соответствовать
интенсивности изменения изучаемого
объекта.3)числовые уровни рядов динамики
должны быть упорядочены во времени, не
допускается анализ рядов динамики с
пропуском во времени.
