8 Упругие силы

Электромагнитные силы в механике проявляют себя как упругие силы и силы трения. Под действием внешних сил возникают деформации (т.е. изменение размеров и формы) тел. Если после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела, то деформация называется упругой. Деформация имеет упругий характер в случае, если внешняя сила не превосходит определенного значения, называемого пределом упругости. При превышении этого предела деформация становится пластичной, или неупругой, т.е. первоначальные размеры и форма тела полностью не восстанавливаются. Рассмотрим упругие деформации. В деформированном теле (рис. 4.2) возникают упругие силы, уравновешивающие внешние силы. Под действием внешней силы –  F_вн  пружина получает удлинение  x, в результате в ней возникает упругая сила –  F_упр, уравновешивающая  F_вн.

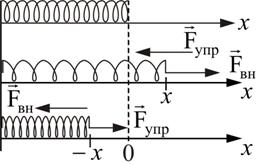Рис. 4.2 Упругие силы возникают во всей деформированной пружине. Любая часть пружины действует на другую часть с силой упругости  F_упр. длинение пружины пропорционально внешней силе и определяется законом Гука: k  – жесткость пружины. Видно, что чем больше  k, тем меньшее удлинение получит пружина под действием данной силы Так как упругая сила отличается от внешней только знаком, т.е.  F_упр = –F_вн, закон Гука можно записать в виде

, F_упр = –kx. Потенциальная энергия упругой пружины равна работе, совершенной над пружиной.        Так как сила непостоянна, элементарная работа  dA = F dx, или dA = –kx dx. Тогда полная работа, которая совершена пружиной, равна:

Сдвиг — в сопротивлении материалов — вид продольной деформации бруса, возникающий в том случае, если сила прикладывается касательно его поверхности (при этом нижняя часть бруска закреплена неподвижно).

Относительная деформация сдвига определяется по формуле

,

где Δx — абсолютный сдвиг параллельных слоёв тела относительно друг друга; l — расстояние между слоями (для малых углов ) Круче́ние — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил (момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор — крутящий момент. На кручение работают пружины растяжения-сжатия и валы.

При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию.Угол закручивания цилиндрического стержня в границах упругих деформаций под действием момента T может быть определён из уравнения закона Гука для случая кручения где:  — геометрический полярный момент инерции;  — длина стержня;G — модуль сдвига.Отношение угла закручивания φ к длине называют относительным углом закручивания Деформация кручения является частным случаем деформации сдвига.

9 Основные дифференциальные операторы

Градие́нт (от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины , значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении. Например, если взять в качестве высоту поверхности Земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона. С математической точки зрения градиент — это производная скалярной функции, определенной на векторном пространстве. Пространство, на котором определена функция и её градиент может быть вообще говоря как обычным трехмерным пространством, так и пространством любой другой разменрости любой физической природы или чисто абстрактным. Стандартные обозначения: или, с использованием оператора набла,

— вместо может быть любое скалярное поле, обозначенное любой буквой, например  — обозначения градиента поля V. Определение Для случая трёхмерного пространства градиентом скалярной функции координат , , называется векторная функция с компонентами , , .Или, использовав для единичных векторов по осям прямоугольных декартовых координат : Если  — функция переменных , то её градиентом называется -мерный вектор

компоненты которого равны частным производным по всем её аргументам.

Размерность вектора градиента определяется, таким образом, размерностью пространства (или многообразия), на котором задано скалярное поле, о градиенте которого идет речь. Оператором градиента (обозначаемым обычно, как говорилось выше, или ) называется оператор, действие которого на скалярную функцию (поле) дает ее градиент. Этот оператор иногда коротко называют просто "градиентом". Смысл градиента любой скалярной функции в том, что его скалярное произведение с бесконечно малым вектором перемещения дает полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена , то есть линейную (в случае общего положения она же главная) часть изменения при смещении на . Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:

Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат , то есть от природы параметров x вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат, а поскольку  — это вектор, то градиент, вычисленный обычным образом, оказывается ковариантным вектором, то есть вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного), то есть вектором, записанным в обычном базисе. Таким образом, выражение (вообще говоря — для произвольных криволинейных координат) может быть вполне правильно и инвариантно записано как:

или, опуская по правилу Эйнштейна знак суммы,

(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше). Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.

Пример

Например, градиент функции будет представлять собой: