5 Масса на основе 2 закона ньютона

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления .инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО). В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе При подходящем выборе единиц измерения, этот закон можно записать в виде формулы: где  — ускорение материальной точки;  — сила, приложенная к материальной точке;  — масса материальной точки. В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс: В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил. где  — импульс точки, где  — скорость точки;  — время;  — производная импульса по времени. Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:

или

Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности. Нельзя рассматривать частный случай (при ) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

6 Сила тяжести вес тела

Закон всемирного тяготения.

В рамках классической механики гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы и , разделёнными расстоянием , пропорциональна обеим массам и обратно пропорциональна квадрату расстояния — то есть:

Здесь  — гравитационная постоянная, равная примерно 6,6725×10^-11 м³/(кг·с²).

Гравитационное поле, так же как и поле силы тяжести, потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность гравитационного поля влечёт за собой закон сохранения суммы кинетической и потенциальной энергии и при изучении движения тел в гравитационном поле часто существенно упрощает решение. В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал зависит только от положения тела в данный момент времени. Большие космические объекты — планеты, звезды и галактики имеют огромную массу и, следовательно, создают значительные гравитационные поля. Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях, и все массы положительны, это, тем не менее, очень важная сила во Вселенной. В частности, электромагнитное взаимодействие между телами на космических масштабах мало, поскольку полный электрический заряд этих тел равен нулю (вещество в целом электрически нейтрально). Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.

Вес — сила воздействия тела на опору (или подвес или другой вид крепления), препятствующую падению, возникающая в поле сил тяжести. (В случае нескольких опор под весом понимается суммарная сила, действующая на все опоры; впрочем, для жидких и газообразных опор в случае погружения тела в них часто делается исключение, т.е. тогда силы воздействие тела на них исключают из веса и включают в силу Архимеда). Единица измерения веса в СИ — ньютон, иногда используется единица СГС — дина. Вес P тела, покоящегося в инерциальной системе отсчёта совпадает с силой тяжести, действующей на тело, и пропорционален массе и ускорению свободного падения в данной точке: Значение веса (при неизменной массе тела) пропорционально ускорению свободного падения, которое зависит от высоты над земной поверхностью (или поверхностью другой планеты, если тело находится вблизи нее, а не Земли, и массы и размеров этой планеты), и, ввиду несферичности Земли, а также ввиду ее вращения (см. ниже), от географических координат точки измерения. Другим фактором, влияющим на ускорение свободного падения и, соответственно, вес тела, являются гравитационные аномалии, обусловленные особенностями строения земной поверхности и недр в окрестностях точки измерения. При движении системы тело — опора (или подвес) относительно инерциальной системы отсчёта c ускорением вес перестаёт совпадать с силой тяжести: В результате суточного вращения Земли существует широтное уменьшение веса: на экваторе примерно на 0,3 % меньше, чем на полюсах.

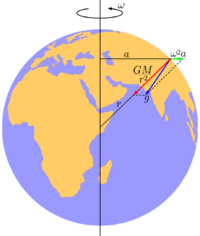
Широтное уменьшение веса. Вес можно измерять с помощью пружинных весов, которые могут служить и для косвенного измерения массы, если их соответствующим образом проградуировать; рычажные весы в такой градуировке не нуждаются, так как в этом случае сравниваются массы, на которые действует одинаковое ускорение свободного падения или сумма ускорений в неинерциальных системах отсчёта. При взвешивании с помощью технических пружинных весов вариациями ускорения свободного падения обычно пренебрегают, так как влияние этих вариаций обычно меньше практически необходимой точности взвешивания. На вес тела в жидкой или газообразной среде влияет также сила Архимеда, таким образом, вес тела, погружённого в среду, уменьшается на вес вытесненного объёма среды; в случае, если плотность тела меньше плотности среды, вес становится отрицательным (то есть на тело действует выталкивающая сила). Сила Архимеда может оказать влияние и на взвешивание с помощью рычажных весов, если сравниваются тела с различной плотностью.Состояние отсутствия веса (невесомость) наступает при удалении тела от притягивающего объекта, либо когда тело находится в свободном падении, то есть .