41 Статистическое определение энтропии

Пусть имеется замкнутая система из N частиц, взаимодействующих между собой посредством консервативных сил, совершающих движение в ограниченной области пространства и обладающих суммарной энергией Е. Все возможные состояния этой системы изображаются точками в фазовом пространстве с размерностью 6N, которые распределены в некоторой области G этого пространства, задаваемой энергией системы. Разделим область G на s одинаковых по объему ячеек , i=1,2,3,…,s таким образом, что энергия частицы в i-ой ячейке равна . Микросостояние задается путем указания конкретных ячеек, в которых находится каждая из N частиц. Макросостояние определяется полным набором чисел частиц , находящихся во всех s ячейках. Статистический вес макросостояния по определению равен числу всех возможных микросостояний, реализующих заданное макросостояние при фиксированных s, N, E и G. Л.Больцман принял одинаковую вероятность реализации любого микросостояния, возможного для заданного макросостояния, и определил термодинамическую вероятность макросостояния на основе формулы Здесь термодинамическая вероятность может принимать значения много больше 1. Используя термодинамическую вероятность (10.1), Л.Больцман дал статистическое (вероятностное) определение энтропии S макросостояния с помощью выражения где k – постоянная Больцмана. Натуральный логарифм в (10.2) обеспечивает аддитивность энтропий подсистем полной системы, поскольку статистический вес полной системы равен произведению статистических весов ее макроскопических подсистем. В соответствии со вторым началом термодинамики энтропия равновесного состояния замкнутой системы принимает максимальное значение. Следовательно, статистический вес и термодинамическая вероятность равновесного состояния также максимальные. Условие максимума статистического веса макросостояния позволяет найти наиболее вероятные распределения частиц по ячейкам фазового пространства и, соответственно, по энергиям как в классической, так и в квантовой физике. В случае классической статистики Больцмана частицы считаются одинаковыми, но различимыми и можно проследить за траекторией движения каждой частицы. Следовательно, перестановки частиц между различными ячейками фазового пространства приводят к новым микросостояниям для заданного макросостояния. Для макросостояния с известными числами статистический вес определяется выражением Здесь учтено, что перестановки частиц в пределах отдельной ячейки не дают новые микросостояния.       Максимум статистического веса ищется при двух дополнительных условиях

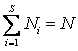
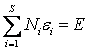
задающих полное число частиц N в системе и их суммарную энергию E. Если принять, что все числа и использовать формулу Стирлинга то условный максимум выражения (10.3) получается при Здесь - наиболее вероятное (среднее) число частиц в i –ой ячейке фазового пространства, μ – химический потенциал системы (нормировочная постоянная, связанная с полным числом частиц) и Т – температура равновесного состояния, зависящая от полной энергии системы. Таким образом, получается уже известный закон распределения Больцмана для классических частиц.