
- •1 Кинематика материальной точки
- •2 Линейные скорость и ускорение
- •3 Вращательное движение, угловая скорость
- •4 Законы классической механики
- •5 Масса на основе 2 закона ньютона
- •6 Сила тяжести вес тела
- •7 Силы трения
- •8 Упругие силы
- •9 Основные дифференциальные операторы
- •10 Консервативные и неконсервативные силы
- •11 Закон сохранения импульса
- •12 Уравнение движения тела переменной массы
- •13 Абсолютно упругий и неупругий удар, нецентральный удар
- •14 Закон сохранения механической энергии
- •1.20. Закон сохранения механической энергии
- •15 Динамика вращательного движения
- •16 Тензор момента инерции
- •17 Свободные оси гироскоп
- •18 Неинерциальная система отсчёта
- •20 Энергия работа мощность
- •21 Преобразования галилея
- •22 Преобразования лоуренца
- •23 Следствия преобразования лоренца
- •24 Реалитивистская энергия и масса
- •25 Интервал в релитивистской механики
- •26 Гравитационное красное смещение
- •27 Элементы механики жидкости
- •Гидро- и аэродинамика Основные понятия
- •28 Уравнение бернули
- •29 Следствие уравнения бернули
- •30 Уравнение неразрывности
- •31 Подъёмная сила крыла самолёта
- •32 Вязкость жидкости
- •33 Закон идеального газа
- •Равнение мкт идеального газа
- •35 Распределение максвелла р аспределение Максвелла
- •36 Распределение больцмана
- •37 Реальный газ
- •38 Первое начало термодинамики
- •39 Уравнение адиабатического процесса
- •40 Второе начало термодинамики
- •41 Статистическое определение энтропии
- •42 Цикл карно
- •43 Длина свободного пробега молекул явление переноса
- •44 Твёрдые тела кристаллы
- •45 Капилярное явление ,поверхностное натяжение
39 Уравнение адиабатического процесса
Адиабатический процесс и политропный процесс
Адиабатическим
называется процесс, при котором
отсутствует теплообмен (Q=0)
между
системой и окружающей средой. К
адиабатическим процессам можно отнести
все быстропротекающие процессы. Например,
адиабатическим процессом можно считать
процесс распространения звука в среде,
так как скорость распространения
звуковой волны настолько велика, что
обмен энергией между волной и средой
произойти не успевает. Адиабатические
процессы применяются в двигателях
внутреннего сгорания (расширение и
сжатие горючей смеси в цилиндрах), в
холодильных установках и т. д.Из первого
начала термодинамики (Q=dU+A)
для адиабатического процесса следует,
что![]() т.
е. внешняя работа совершается за счет
изменения внутренней энергии
системы.Используя выражения (52.1) и
(53.4), для произвольной массы газа перепишем
уравнение (55.1) в виде
т.
е. внешняя работа совершается за счет
изменения внутренней энергии
системы.Используя выражения (52.1) и
(53.4), для произвольной массы газа перепишем
уравнение (55.1) в виде![]() Продифференцировав
уравнение состояния для идеального
газа
Продифференцировав
уравнение состояния для идеального
газа
![]() получим
получим![]() Исключим
из (55.2) и (55.3) температуру Т.
Исключим
из (55.2) и (55.3) температуру Т.
![]() Разделив
переменные и учитывая, что Сp/СV=
(см.
(53.8)), найдем
Разделив
переменные и учитывая, что Сp/СV=
(см.
(53.8)), найдем![]() Интегрируя
это уравнение в пределах от p1
до p2
и соответственно от V1
до V2,
а затем потенцируя, придем к выражению
Интегрируя
это уравнение в пределах от p1
до p2
и соответственно от V1
до V2,
а затем потенцируя, придем к выражению![]() Так
как состояния 1
и 2
выбраны произвольно, то можно
записать
Так
как состояния 1
и 2
выбраны произвольно, то можно
записать![]() Полученное
выражение есть
уравнение адиабатического процесса,
называемое также уравнением
Пуассона.Для
перехода к переменным Т,
V
или
p,
Т исключим
из (55.4) с помощью уравнения Клапейрона
— Менделеева
Полученное
выражение есть
уравнение адиабатического процесса,
называемое также уравнением
Пуассона.Для
перехода к переменным Т,
V
или
p,
Т исключим
из (55.4) с помощью уравнения Клапейрона
— Менделеева![]() соответственно
давление или объем:
соответственно
давление или объем:
![]()
![]() Выражения
(55.4) — (55.6) представляют собой уравнения
адиабатического процесса. В этих
уравнениях безразмерная величина (см.
(53.8) и (53.2))
Выражения
(55.4) — (55.6) представляют собой уравнения
адиабатического процесса. В этих
уравнениях безразмерная величина (см.
(53.8) и (53.2))
![]() называется
показателем адиабаты
(или
коэффициентом Пуассона).
Для одноатомных газов (Ne,
He
и др.), достаточно хорошо удовлетворяющих
условию идеальности, i=3,
=1,67.
Для двухатомных газов (Н2, N2,
О2 и др.) i=5,
=1,4.
Значения ,
вычисленные по формуле (55.7), хорошо
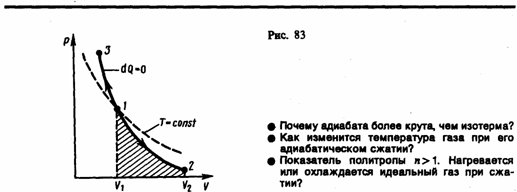
подтверждаются экспериментом. Диаграмма
адиабатического процесса (адиабата)
в координатах р,
V
изображается гиперболой (рис. 83). На
рисунке видно, что адиабата (pV
=
const)
более крута, чем изотерма (pV
=
const).
Это объясняется тем, что при адиабатическом
сжатии 1—3
увеличение
давления газа обусловлено не только
уменьшением его объема, как при
изотермическом сжатии, но и повышением
температуры.Вычислим работу, совершаемую
газом в адиабатическом процессе. Запишем
уравнение (55.1) в виде
называется
показателем адиабаты
(или
коэффициентом Пуассона).
Для одноатомных газов (Ne,
He
и др.), достаточно хорошо удовлетворяющих
условию идеальности, i=3,
=1,67.
Для двухатомных газов (Н2, N2,
О2 и др.) i=5,
=1,4.
Значения ,
вычисленные по формуле (55.7), хорошо
подтверждаются экспериментом. Диаграмма
адиабатического процесса (адиабата)
в координатах р,
V
изображается гиперболой (рис. 83). На
рисунке видно, что адиабата (pV
=
const)
более крута, чем изотерма (pV
=
const).
Это объясняется тем, что при адиабатическом
сжатии 1—3
увеличение
давления газа обусловлено не только
уменьшением его объема, как при
изотермическом сжатии, но и повышением
температуры.Вычислим работу, совершаемую
газом в адиабатическом процессе. Запишем
уравнение (55.1) в виде![]() Если
газ адиабатически расширяется от объема
V1
до V2,
то его температура уменьшается от
T1
до T2
и работа расширения идеального
газа
Если
газ адиабатически расширяется от объема
V1
до V2,
то его температура уменьшается от
T1
до T2
и работа расширения идеального
газа![]() Применяя
те же приемы, что и при выводе формулы
(55.5), выражение (55.8) для работы при
адиабатическом расширении можно
преобразовать к виду
Применяя
те же приемы, что и при выводе формулы
(55.5), выражение (55.8) для работы при
адиабатическом расширении можно
преобразовать к виду![]() где
где
![]() .
.
Работа,
совершаемая газом при адиабатическом
расширении 1—2
(определяется площадью, заштрихованной
на рис. 83), меньше, чем при изотермическом.
Это объясняется тем, что при
адиабатическом расширении происходит
охлаждение газа, тогда как при
изотермическом — температура
поддерживается постоянной за счет
притока извне эквивалентного количества
теплоты.Рассмотренные изохорный,
изобарный, изотермический и адиабатический
процессы имеют общую особенность — они
происходят при постоянной теплоемкости.
В первых двух процессах теплоемкости
соответственно равны СV
и Сp,
в изотермическом процессе (dT=0)
теплоемкость равна ±,
в адиабатическом (Q=0)
теплоемкость равна нулю. Процесс, в
котором теплоемкость остается постоянной,
называется политропным.
 Исходя
из первого начала термодинамики при
условии постоянства теплоемкости
(C=const)
можно вывести уравнение политропы:
Исходя
из первого начала термодинамики при
условии постоянства теплоемкости
(C=const)
можно вывести уравнение политропы:
![]() где
п=(С—Сp)/(С—СV)—показатель
политропы. Очевидно, что при С=0,
n=,
из (55.9) получается уравнение адиабаты;
при С
=
,
n
= 1 — уравнение изотермы; при С=Сp,
n=0
—уравнение изобары, при С=СV,
n=±
— уравнение изохоры. Таким образом, все
рассмотренные процессы являются частными
случаями политропного процесса.
где
п=(С—Сp)/(С—СV)—показатель
политропы. Очевидно, что при С=0,
n=,
из (55.9) получается уравнение адиабаты;
при С
=
,
n
= 1 — уравнение изотермы; при С=Сp,
n=0
—уравнение изобары, при С=СV,
n=±
— уравнение изохоры. Таким образом, все
рассмотренные процессы являются частными
случаями политропного процесса.
