
- •1 Кинематика материальной точки
- •2 Линейные скорость и ускорение
- •3 Вращательное движение, угловая скорость
- •4 Законы классической механики
- •5 Масса на основе 2 закона ньютона
- •6 Сила тяжести вес тела
- •7 Силы трения
- •8 Упругие силы
- •9 Основные дифференциальные операторы
- •10 Консервативные и неконсервативные силы
- •11 Закон сохранения импульса
- •12 Уравнение движения тела переменной массы
- •13 Абсолютно упругий и неупругий удар, нецентральный удар
- •14 Закон сохранения механической энергии
- •1.20. Закон сохранения механической энергии
- •15 Динамика вращательного движения
- •16 Тензор момента инерции
- •17 Свободные оси гироскоп
- •18 Неинерциальная система отсчёта
- •20 Энергия работа мощность
- •21 Преобразования галилея
- •22 Преобразования лоуренца
- •23 Следствия преобразования лоренца
- •24 Реалитивистская энергия и масса
- •25 Интервал в релитивистской механики
- •26 Гравитационное красное смещение
- •27 Элементы механики жидкости
- •Гидро- и аэродинамика Основные понятия
- •28 Уравнение бернули
- •29 Следствие уравнения бернули
- •30 Уравнение неразрывности
- •31 Подъёмная сила крыла самолёта
- •32 Вязкость жидкости
- •33 Закон идеального газа
- •Равнение мкт идеального газа
- •35 Распределение максвелла р аспределение Максвелла
- •36 Распределение больцмана
- •37 Реальный газ
- •38 Первое начало термодинамики
- •39 Уравнение адиабатического процесса
- •40 Второе начало термодинамики
- •41 Статистическое определение энтропии
- •42 Цикл карно
- •43 Длина свободного пробега молекул явление переноса
- •44 Твёрдые тела кристаллы
- •45 Капилярное явление ,поверхностное натяжение
37 Реальный газ
Реальный
газ —
газ,
который не описывается уравнением
состояния идеального газа Клапейрона —
Менделеева.Зависимости
между его параметрами показывают, что
молекулы в реальном газе взаимодействуют
между собой и занимают определенный
объём. Состояние реального газа часто
на практике описывается обобщённым
уравнением Менделеева — Клапейрона:
![]() где
p — давление; V - объем T — температура;
Zr
= Zr
(p,T) — коэффициент
сжимаемости
газа; m - масса; М — молярная
масса;
R — газовая
постоянная.
Уравнение состояния газа Ван-дер-Ваальса —
уравнение,
связывающее основные термодинамические
величины
в модели газа Ван-дер-Ваальса.Хотя
модель идеального
газа
хорошо описывает поведение реальных
газов
при низких давлениях
и высоких температурах,
в других условиях её соответствие с
опытом
гораздо хуже. В частности, это проявляется
в том, что реальные
газы
могут быть переведены в жидкое
и даже в твёрдое
состояние,
а идеальные — не могут.Для более
точного описания поведения реальных
газов при низких температурах была
создана модель газа Ван-дер-Ваальса,
учитывающая силы межмолекулярного
взаимодействия. В этой модели внутренняя
энергия
где
p — давление; V - объем T — температура;
Zr
= Zr
(p,T) — коэффициент
сжимаемости
газа; m - масса; М — молярная
масса;
R — газовая
постоянная.
Уравнение состояния газа Ван-дер-Ваальса —
уравнение,
связывающее основные термодинамические
величины
в модели газа Ван-дер-Ваальса.Хотя
модель идеального
газа
хорошо описывает поведение реальных
газов
при низких давлениях
и высоких температурах,
в других условиях её соответствие с
опытом
гораздо хуже. В частности, это проявляется
в том, что реальные
газы
могут быть переведены в жидкое
и даже в твёрдое
состояние,
а идеальные — не могут.Для более
точного описания поведения реальных
газов при низких температурах была
создана модель газа Ван-дер-Ваальса,
учитывающая силы межмолекулярного
взаимодействия. В этой модели внутренняя
энергия
![]() становится
функцией не только температуры,
но и объёма.
становится
функцией не только температуры,
но и объёма.
Уравнение состоянияТермическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.Для одного моля газа Ван-дер-Ваальса оно имеет вид:
![]()
где — давление, — молярный объём — абсолютная температура, — универсальная газовая постоянная.
Видно,
что это уравнение фактически является
уравнением
состояния идеального газа
с двумя поправками. Поправка
учитывает
силы притяжения между молекулами
(давление на стенку уменьшается, т.к.
есть силы, втягивающие молекулы
приграничного слоя внутрь), поправка
![]() —
силы отталкивания (из общего объёма
вычитаем объём, занимаемый молекулами).Для
молей
газа Ван-дер-Ваальса уравнение состояния
выглядит так:
—
силы отталкивания (из общего объёма
вычитаем объём, занимаемый молекулами).Для
молей
газа Ван-дер-Ваальса уравнение состояния
выглядит так:
![]() где
—
объём,
где
—
объём,
Внутренняя
энергия газа Ван-дер-ВаальсаПотенциальная
энергия межмолекулярных сил взаимодействия
вычисляется как работа, которую совершают
эти силы, при разведении молекул на
бесконечность:
![]() Внутренняя
энергия
газа Ван-дер-Ваальса складывается из
его кинетической энергии (энергии
теплового движения молекул) и только
что нами посчитанной потенциальной.
Так, для одного моль газа:
Внутренняя
энергия
газа Ван-дер-Ваальса складывается из
его кинетической энергии (энергии
теплового движения молекул) и только
что нами посчитанной потенциальной.
Так, для одного моль газа:
![]() где
где
![]() —
молярная
теплоёмкость
при постоянном объёме, которая
предполагается не зависящей от
температуры.
—
молярная
теплоёмкость
при постоянном объёме, которая
предполагается не зависящей от
температуры.
38 Первое начало термодинамики
Существует
несколько эквивалентных формулировок
первого начала термодинамикиВ любой
изолированной системе запас энергии
остаётся постоянным.[2]
Это — формулировка Дж.
П. Джоуля
(1842 г.).Количество
теплоты,
полученное системой, идёт на изменение
её внутренней энергии и совершение
работы против внешних силИзменение
внутренней энергии системы при переходе
её из одного состояния в другое равно
сумме работы внешних сил и количества
теплоты, переданного системе, то есть,
оно зависит только от начального и
конечного состояния системы и не зависит
от способа, которым осуществляется этот
переход. Это определение особенно важно
для химической термодинамики[2]
(ввиду сложности рассматриваемых
процессов). Иными словами, внутренняя
энергия является функцией состояния.
В циклическом процессе внутренняя
энергия не изменяется.
![]() Изменение
полной энергии системы в квазистатическом
процессе
равно количеству теплоты
,
сообщённому системе, в сумме с изменением
энергии, связанной с количеством
вещества
Изменение
полной энергии системы в квазистатическом
процессе
равно количеству теплоты
,
сообщённому системе, в сумме с изменением
энергии, связанной с количеством
вещества
![]() при
химическом
потенциале
,
и работы
при
химическом
потенциале
,
и работы
![]() [3],
совершённой над системой внешними
силами и полями,
за вычетом работы
,
совершённой самой системой против
внешних сил
[3],
совершённой над системой внешними
силами и полями,
за вычетом работы
,
совершённой самой системой против
внешних сил![]() Для
элементарного количества теплоты
Для
элементарного количества теплоты
![]() ,
элементарной работы
,
элементарной работы
![]() и
малого приращения
и
малого приращения
![]() внутренней
энергии первый закон термодинамики
имеет вид:
внутренней
энергии первый закон термодинамики
имеет вид:
![]()
Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствие разных источников сил.
Важно
заметить, что
и
![]() являются
полными
дифференциалами,
а
и
—
нет.
являются
полными
дифференциалами,
а
и
—
нет.
Применение
первого начала термодинамики к
изопроцессамСреди
равновесных процессов, происходящих с
термодинамическими системами, выделяются
изопроцессы,
при которых один из основных параметров
состояния сохраняется постоянным.Изохорный
процесс
(V=const).
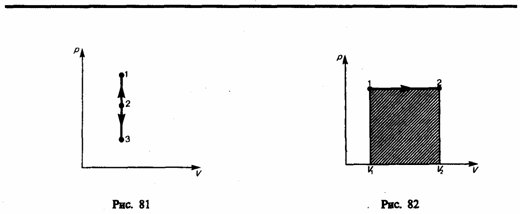
Диаграмма этого процесса
(изохора) в
координатах р,
V
изображается прямой, параллельной оси
ординат (рис. 81), где процесс 1—2
есть изохорное нагревание, а 1—3
—
изохорное охлаждение. При изохорном
процессе газ не совершает работы над
внешними телами, т. е.
![]() Как
уже указывалось в § 53, из первого начала
термодинамики (Q=dU+A)
для
изохорного
процесса следует, что вся теплота,
сообщаемая газу, идет на увеличение его
внутренней энергии:
Как
уже указывалось в § 53, из первого начала
термодинамики (Q=dU+A)
для
изохорного
процесса следует, что вся теплота,
сообщаемая газу, идет на увеличение его
внутренней энергии:
![]() Согласно
формуле
Согласно
формуле
![]() Тогда
для произвольной массы газа
получим
Тогда
для произвольной массы газа
получим![]()
 Изобарный
процесс
(p=const).
Диаграмма этого процесса (изобара) в
координатах р,
V
изображается прямой, параллельной оси
V.
При изобарном процессе работа газа (см.
(52.2)) при увеличения объема от V1
до V2
равна
Изобарный
процесс
(p=const).
Диаграмма этого процесса (изобара) в
координатах р,
V
изображается прямой, параллельной оси
V.
При изобарном процессе работа газа (см.
(52.2)) при увеличения объема от V1
до V2
равна![]() и
определяется площадью заштрихованного
прямоугольника (рис. 82). Если использовать
уравнение (42.5) Клапейрона — Менделеева
для выбранных нами двух состояний,
то
и
определяется площадью заштрихованного
прямоугольника (рис. 82). Если использовать
уравнение (42.5) Клапейрона — Менделеева
для выбранных нами двух состояний,
то![]() откуда
откуда![]() Тогда
выражение (54.2) для работы изобарного
расширения примет вид
Тогда
выражение (54.2) для работы изобарного
расширения примет вид![]() Из
этого выражения вытекает физический
смысл
молярной газовой постоянной R:
если
T2
—T1
=1
К, то для 1 моль газа R=A,
т. е. R
численно равна работе изобарного
расширения 1 моль идеального газа при
нагревании его на 1 К.В изобарном процессе
при сообщении газу массой т
количества теплоты
Из
этого выражения вытекает физический
смысл
молярной газовой постоянной R:
если
T2
—T1
=1
К, то для 1 моль газа R=A,
т. е. R
численно равна работе изобарного
расширения 1 моль идеального газа при
нагревании его на 1 К.В изобарном процессе
при сообщении газу массой т
количества теплоты![]() его
внутренняя энергия возрастает на
величину (согласно формуле (53.4))
его
внутренняя энергия возрастает на
величину (согласно формуле (53.4))
![]() При
этом газ совершит работу, определяемую
выражением (54.3). Изотермический
процесс
(T=const).
Как уже указывалось, изотермический
процесс описывается законом Бойля—Мариотта:
При
этом газ совершит работу, определяемую
выражением (54.3). Изотермический
процесс
(T=const).
Как уже указывалось, изотермический
процесс описывается законом Бойля—Мариотта:
![]()
 Диаграмма
этого процесса (изотерма)
в координатах р,
V
представляет собой гиперболу (см. рис.
60), расположенную на диаграмме тем выше,
чем выше температура, при которой
происходит процесс.Исходя из выражений
(52.2) и (42.5) найдем работу изотермического
расширения газа:
Диаграмма
этого процесса (изотерма)
в координатах р,
V
представляет собой гиперболу (см. рис.
60), расположенную на диаграмме тем выше,
чем выше температура, при которой
происходит процесс.Исходя из выражений
(52.2) и (42.5) найдем работу изотермического
расширения газа:
![]() Так
как при Т=const
внутренняя энергия идеального газа не
изменяется:
Так
как при Т=const
внутренняя энергия идеального газа не
изменяется:
![]() то
из первого начала термодинамики
(Q=dU+A)
следует, что для изотермического
процесса
то
из первого начала термодинамики
(Q=dU+A)
следует, что для изотермического
процесса![]() т.
е. все количество теплоты, сообщаемое
газу, расходуется на совершение им
работы против внешних сил:
т.
е. все количество теплоты, сообщаемое
газу, расходуется на совершение им
работы против внешних сил:
![]() Следовательно,
для того чтобы при расширении газа
температура не понижалась, к газу в
течение изотермического процесса
необходимо подводить количество теплоты,
эквивалентное внешней работе расширения.
Следовательно,
для того чтобы при расширении газа
температура не понижалась, к газу в
течение изотермического процесса
необходимо подводить количество теплоты,
эквивалентное внешней работе расширения.
