1 Кинематика материальной точки

Кинема́тика точки  — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.Движение любого объекта в кинематике изучают по отношению к некоторой системе отсчета, включающей:Тело отсчета;Систему измерения положения тела в пространстве (систему координат);Прибор для измерения времени (Часы).Положение точки определяется набором обобщенных координат — упорядоченным набором числовых величин, полностью описывающих положение тела. В самом простом случае это координаты точки (радиус-вектора) в выбранной системе координат. Наиболее наглядное представление о радиус-векторе можно получить в евклидовой системе координат, поскольку базис в ней является фиксированным и общим для любого положения тела.

Кинематика поступательного движенияОсновные кинематические понятия

Материальная точка  — тело, размерами которого по сравнению с характерными расстояниями данной задачи можно пренебречь. При поступательном движении в ряде случаев при помощи понятия М. Т. можно описывать и изменение положения более крупных объектов.

Радиус-вектор — Вектор, определяющий положение М. Т. в пространстве: . Здесь  — координаты радиус-вектора. Геометрически изображается вектором, проведенным из начала координат к материальной точке. Зависимость радиус-вектора (или его координат ) от времени называется законом движения.Траектория — Годограф радиус-вектора, то есть — воображаемая линия, описываемая концом радиус-вектора в процессе движения. Иными словами, траектория — это линия вдоль которой движется М. Т. При этом закон движения выступает как уравнение, задающее траекторию параметрически. Длину участка траектории между начальным и конечным моментами времени часто называют пройденным расстоянием, длиной пути или вульгарно — путем и обозначают буквой S. При таком описании движения S выступает в качестве обобщенной координаты, а законы движения в этом случае записывается в виде S = S(t) и аналогичны соответствующим законам для координат. Например закон равноускоренного криволинейного движения может быть записан в виде:

,

Где :  — модуль начальной скорости, а  — Тангенциальное ускорение.Описание движения при помощи понятия траектории — один из ключевых моментов классической механики . В квантовой механике движения носит бестраекторный характер, а само понятие траектории теряет смысл.Основные кинематические величины

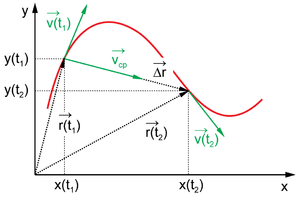Радиус-вектора и вектор перемещения (черные стрелки). Вектора средней и мгновенных скоростей (Зеленые стрелки). Траектория (красная линия)

Разложение ускорения по сопутствующему базису Перемещение — векторная физическая величина, равная разности радиус-векторов в конечный и начальный моменты времени:

. Иными словами, перемещение — это приращение радиус-вектора за выбранный промежуток времени. Средняя скорость — векторная физическая величина равная отношению вектора перемещения к промежутку времени, за который происходит это перемещение:

.Мгновенная скорость — векторная физическая величина, равная первой производной от радиус-вектора по времени:

.Характеризует быстроту перемещения материальной точки. Мгновенную скорость можно определить как предел средней скорости при устремлении к нулю промежутка времени, на котором она вычисляется:

.Единица измерения скорости в системе СИ— м/с, в системе СГС — см/с. Мгновенная скорость всегда направлена по касательной к траектории. Мгновенное ускорение — векторная физическая величина, равная второй производной от радиус-вектора по времени и, соответственно, первой производной от мгновенной скорости по времени:

.Характеризует быстроту изменения скорости. Единица ускорения в системе СИ— м/с², в системе СГС — см/с². В случае движения в плоскости вектор ускорения можно разложить по сопутствующему базису: на вектор нормального и тангенциального ускорения:

.Здесь  — единичный вектор нормали,  — единичный вектор касательной. Величина называется нормальным ускорением и характеризует скорость изменения направления движения. Нормальное ускорение выражается через мгновенную скорость и радиус кривизны траектории:

.В случае движения по окружности нормальное ускорение называется центростремительным. Как видно из предыдущей формулы, при движении по окружности с постоянной скоростью нормальное ускорение постоянно по модулю и направлено к центру окружности.

Величина называется тангенциальным ускорением и характеризует величину изменения модуля скорости:

.

Преобразования Галилея

Примеры законов движения, описываемых дифференциальными уравнениями второго порядка

Закон равноускоренного движения

Равноускоренное движение в поле тяжести Земли Закон равноускоренного движения получается в результате решения простейшего дифференциального уравнения вида:

Общее решение этого уравнения дается формулой:

 ;Здесь и — произвольные константы, соответствующие начальной координате и начальной скорости. Движение с постоянным ускорением называют равноускоренным. Движение с постоянным ускорением подчиняется закону:

 ;

.При этом уравнения движения в координатной форме имеют аналогичный вид:

 ;

. В этом случае часто говорят о равноускоренном движении, если знаки и совпадают и о равнозамедленном, если и имеют противоположные знаки. При этом знак каждой из величин зависит от начального выбора системы отсчета. Частный случай равноускоренного движения — равномерное движение. В этом случае . Тогда движение описывается закону: