13. Градиент, дивергенция и ротор

 Важнейшими характеристиками скалярных и векторных полей являются градиент (grad) скалярного поля, дивергенция(div) и ротор(rot) векторного поля.

     Определение 3: Градиентом дифференцируемого скалярного поля u(M)=u(x,y,z) называется вектор

Т.е. сумма частных производных умноженных на соответствующие единичные вектора. О производных функии мы писали в предыдущих статьях: Производная функции, Практическое использование понятия: производная функции.

     Определение 4: Дивергенцией (или расходимостью) дифференцируемого векторного поля называется скаляр

     Определение 5: Ротором (или вихрем) дифференцируемого векторного поля   называется вектор

который с помощью символической записи удобно представить в виде векторного произведения

Операторы grad, div,rot называются основными операторами теории поля.

В качестве примеров использования операторов градиента скалярного поля, дивергенции и ротора векторного поля приведем формулу связи напряженности и потенциала электростатического поля: и систему уравнений Максвелла для стационарного электромагнитного поля:

1)

2)

3)

4)

В математической и особенно физической литературе наряду с введенными операторами широко используется символический векторный дифференциальный оператор набла (оператор Гамильтона). Правила работы с оператором Гамильтона такие же, как и с обычными векторами. Выразим операторы поля через оператор Гамильтона. Вычисляя произведение вектора на скалярную функцию u, скалярное и векторное произведения вектора на вектор , получим формулы

14. Уравнение с разделяющимися переменными

Дифференциальное уравнение

(3.1)

называется уравнением с разделяющимися переменными.

Умножая обе части уравнения на 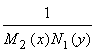, получаем уравнение

(3.2)

В уравнении (3.2) коэффициент при dx зависит только от x, а коэффициент при dy зависит только от y. Значит, в уравнении (3.2) переменные разделены. Интегрируя, получаем:

+

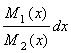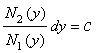
15. Линейные уравнения

В математике линейное дифференциальное уравнение имеет вид

где дифференциальный оператор L линеен, y — неизвестная функция , а правая часть  — функция от той же переменной, что и y.

Линейный оператор L можно рассматривать в форме

Уравнения с переменными коэффициентами

Линейное дифференциальное уравнение порядка n с переменными коэффициентами имеет общий вид

Пример

Уравнение Коши — Эйлера, используемое в инженерии, является простым примером линейного дифференциального уравнения с переменными коэффициентами

Уравнение первого порядка

Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид

Уравнения в такой форме могут быть решены путём умножения на интегрирующий множитель

получим

используем правило дифференцирования произведения

что, после интегрирования обеих частей, дает нам

Таким образом, решение линейного дифференциального уравнения первого порядка

(в частности, с постоянными коэффициентами) имеет вид

где является константой интегрирования.

Пример

Возьмём дифференциальное уравнение первого порядка с постоянными коэффициентами:

Это уравнение имеет особое значение для систем первого порядка, таким как RC-схемы и масс-демпфер^{[неизвестный термин]} системы.

В этом случае, p(x) = b, r(x) = 1.

Следовательно, решение будет: