Раздел 8. Функция распределения и числовые характеристики случайной величины

1. Дана таблица распределения дискретной случайной величины ξ. 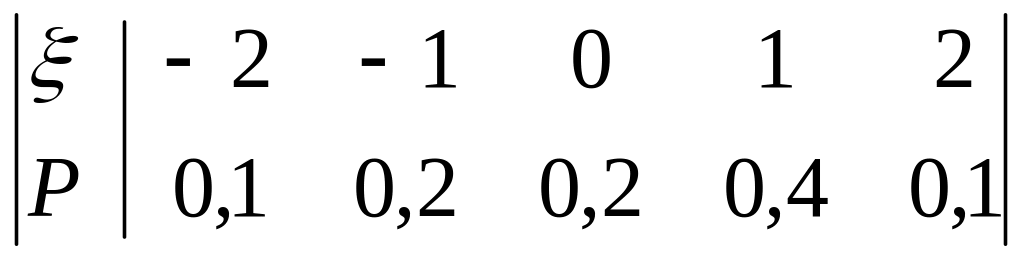. Требуется:

а) построить многоугольник (полигон) распределения;

б) найти функцию распределения и начертить её график;

с) найти

г) найти математическое ожидание, дисперсию, среднеквадратичное отклонение, коэффициент вариации, медиану и моду ξ.

д) таблицу распределения случайной величины

2. В урне 5 белых и 25 чёрных шаров. Из урны наугад вынимают 1 шар. Случайная величина ξ – число вынутых белых шаров. Требуется: а) – д) из задачи 1.

3. Бросают 3 монеты. Случайная величина ξ - число выпавших «гербов». Требуется : а) – д) из задачи 1.

4. В партии из 25 изделий содержится 6 бракованных Для проверки качества из партии случайным образом взяты 3 изделия. Случайная величина ξ – число бракованных изделий в этой выборке. Построить таблицу распределения случайной величины ξ и найти математическое ожидание ξ.

5. Случайная величина ξ задана функцией распределения:

Найти а) плотность распределения ξ; б) вероятность попадания ξ в интервал

(1; 2,5); в) то же в интервал (2,5, 3,5).

6. Случайная величина ξ имеет плотность распределения

Найти: а) функцию распределения ξ ; б) вероятность попадания ξ в интервал

(0; π/4).

7. Математическое ожидание и дисперсия случайной величины ξ равны соответственно 2 и 10. Найти математическое ожидание, дисперсию и среднеквадратичное отклонение случайной величины -4ξ+ 5.

8. Найти математическое ожидание, дисперсию и среднеквадратичное отклонение:

а) числа очков, выпавших при бросании одной игральной кости; б) суммы очков, выпадающих при бросании n игральных костей.

4. Точка случайно бросается в круг радиуса R. Случайная величина ξ – расстояние от брошенной точки до центра круга. Вероятность попадания точки в любую область, расположенную внутри круга, пропорциональна площади этой области. Найти функцию распределения и математическое ожидание случайной величины ξ.

4. Производится опыт, в котором вероятность наступления события А равна р. Случайная величина ξ - число наступления события А в этом опыте. Доказать, что

Раздел 9. Основные типы распределений случайных величин

1. Найти математическое ожидание, дисперсию и среднеквадратичное отклонение числа лотерейных билетов, на которые выпадут выигрыши, если куплено 40 билетов, а вероятность приобретения выигрышного билета равна 0,05.

2. Производится 20 независимых опытов, в каждом из которых вероятность успеха равна 0,2. Найти дисперсию числа успехов в этой серии опытов.

3. Восемьдесят процентов персональных компьютеров безотказно работают в течение 5 лет. Найти вероятность того, что из данных 100 компьютеров не менее 70 проработают 5 лет.

4. Вероятность аварии водопровода в жилом доме в течение года равна 0,02. В районе сто жилых домов. Найти вероятности событий:

А - в течение года в районе не будет аварий водопровода;

В - в течение года в районе произойдёт больше двух аварий водопровода.

5. Случайная величина ξ равномерно распределена на отрезке [1, 11]. Найти плотность распределения ξ, Мξ , Меξ , Моξ , Dξ .

6. В часы пик поезда метро идут с интервалом 45 с. Случайная величина ξ - время ожидания поезда пассажиром. Найти и среднее время ожидания поезда пассажиром.

7. Случайная величина ξ имеет нормальное распределение с параметрами μ = 0,

σ = 1. Найти .

8. Случайная величина ξ имеет нормальное распределение с параметрами μ=2, σ = 3. Найти P(4 < ξ < 5).

9. Случайная величина ξ имеет нормальное распределение с параметрами μ = 1,

σ = 0,5. Найти .

10. Случайная величина ξ имеет нормальное распределение с параметрами μ = 1,

σ =2. Найти .

11. При 10000 бросаниях монеты «герб» выпал 5400 раз. Следует ли считать, что монета несимметрична?

Ответы

Раздел 1

1. а) {ГГГ, ГГР, ГРГ, РГГ, РРГ, РГР, ГРР, РРР},

б) A = {ГРР, РГР, РРГ}, B={ГГР, ГРГ, РГГ}, C={ГГР, ГРГ, РГГ, ГГГ},

в) 3/8, 3/8, 1/2

2.

3. а) нет, б) ,

в)

Раздел 2

1. 3/10, 7/10

2. а) 1/3 , б) 1\2 , в) 0

3. а) 1/6 , б) 1/3 , в) 1/ 2, г) 1/3

4. а) 1/36, б) 1/18, в) 5/18, г) 11/36

5.

6. 

7. 

8. 

9. 

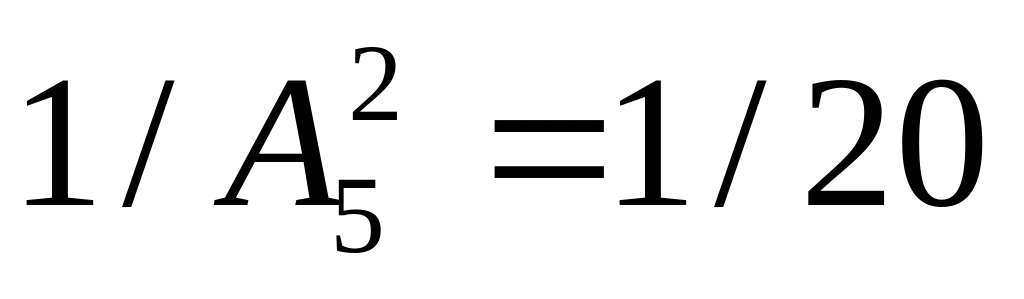
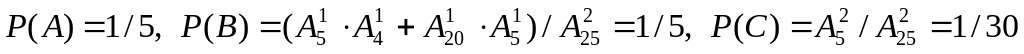
10. (m – 1) / (n – 1)

11. (m – 1) / (n – 1)

12. 

13. 

14. 

15. 

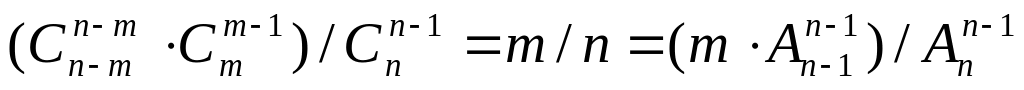
16. ¼

Раздел 3

1. 2/3

2. 2/9 , 1/3

3. Зависимы:

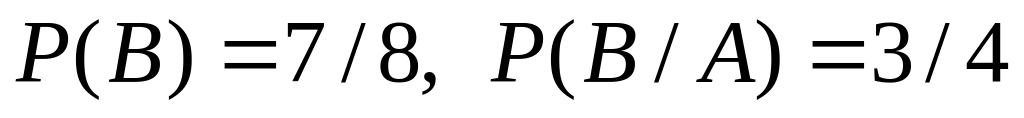
4. Зависимы:

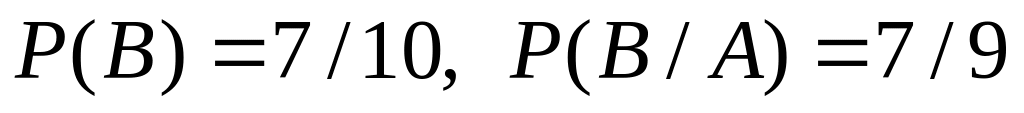
5. 2/3

6. Нет: 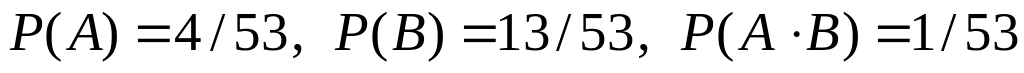, так что

7. 

= поэтому события A, B, C попарно независимы. Но , так что события

A, B, C зависимы в совокупности.

8. 

Раздел 4

1. а) 0,98 , б) 0,26 , в) 0,02

2. 1/126

3. 1/216 , 1/36 ,

1. 5/8

5. 7/9

6. 1/2

7. 28/29 . Замечание: задачу проще решить переходом к противоположному событию.

8. 65/81

9. 0,1. Найти аналогию с «хорошим» билетом на экзамене. 0,5

10. 

11. ,

12. 

13. 

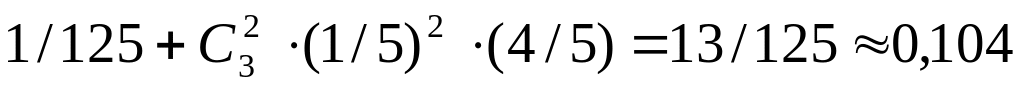
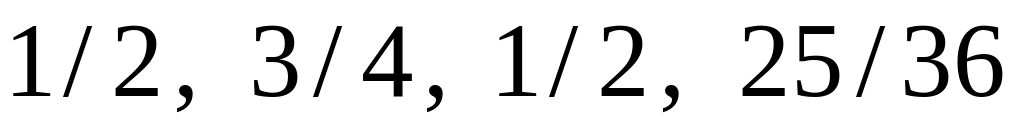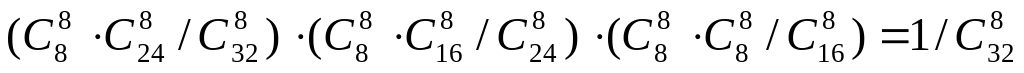
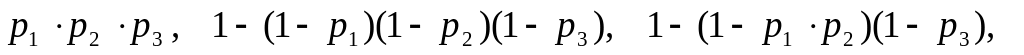
7. В системе 1 : - вероятность работы верхней цепи (из элементов 1, 2) и - вероятность работы нижней цепи (из элементов 3, 4). Поэтому вероятность работы системы 1 равна

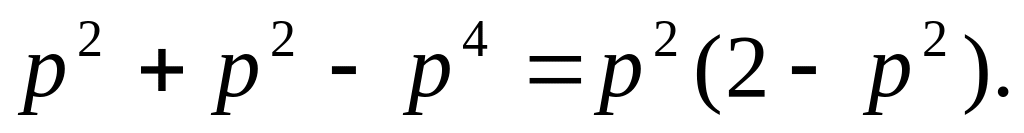
В системе 2: - вероятность работы левого звена (из элементов 1, 3) и - вероятность работы правого звена (из элементов 2, 4). Поэтому вероятность работы системы 2 равна

Следовательно, вторая система надёжнее.

16. Событие А – жюри примет правильное решение – является суммой следующих несовместных событий: (1-ый судья – правильное решение, и 2-ой судья - правильное решение, и 3-ий судья – правильное решение) + (1-ый судья – правильное решение, и 2-ой судья - правильное решение, и 3-ий судья – неправильное решение) + (1-ый судья – неправильное решение, и 2-ой судья - правильное решение, и 3-ий судья – правильное решение) + (1-ый судья – правильное решение, и 2-ой судья - неправильное решение, и 3-ий судья – правильное решение) . Каждое слагаемое в сумме – произведение независимых в совокупности событий. Поэтому:

17. Вероятность принятия жюри правильного решения равна

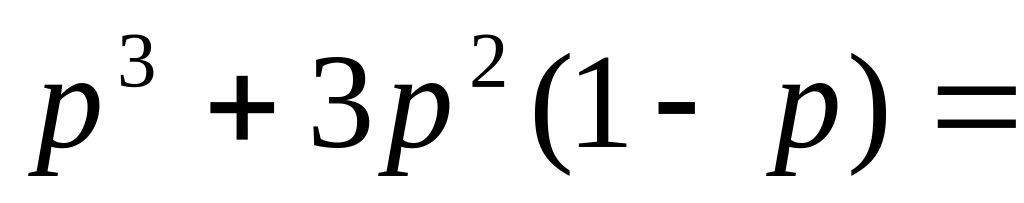
Неравенство выполнено при

18. Вероятность принятия жюри правильного решения равна

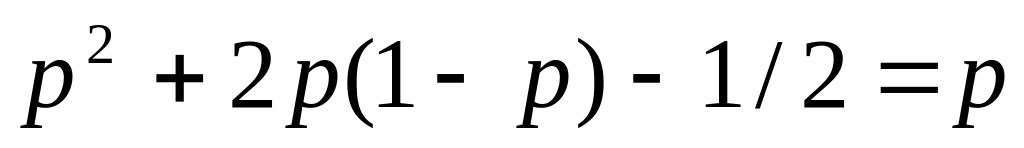
19. 609/625