§ 95. Связь между плотностью газа и давлением

Плотность жидкости мало зависит от давления. Например, при изменении давления на воду в 1000 атм ее объем изменяется только на 5%. Поэтому, если в наших опытах происходят изменения давле­ния не более чем на десятки атмосфер, то почти всегда в гидроста­тике можно при расчетах пренебрегать изменениями объема и считать, что исследуемая жидкость несжимаема.

Плотность  измеряется в различных единицах, размерность которых [m/V]. В системе СИ плотность измеряется в кг/м³, в физиче­ской системе единиц СГС — в единицах г/см³ (в технической систе­ме— в кгс•с²/м⁴). Часто в опытах и расчетах используют вместо плотности понятие удельный вес — вес вещества, содержащегося в единице объема. Удельный вес измеряют обычно в Н/м³, в гс/см³ или в кгс/м³. Удельный вес воды при обычных условиях равен 9800 Н/м³ в системе СИ, 1 гс/см³ в физической системе единиц и примерно 1000 кгс/м^:) в технической системе.

Плотность газов существенно зависит от давления, под которым газ находится. При неизменной температуре плотность газов (или удельный вес) пропорциональна давлению (закон Бойля— Мариотта).

Обозначим начальное давление газа через р_н, соответствующий этому давлению удельный вес — через _н и соответствующее удель­ному весу  какое-то другое давление — через р; тогда закон Бойля—Мариотта запишется так:

(95.1)

Этот закон получен опытным путем, посредством простых опытов, известных из курса физики средней школы, где, однако, обычно связывают давление и объем, занимаемый одной и той же массой газа. Очевидно, что, зная объем и вес газа, легко определить удель­ный Бес (или плотность).

Вспомним также из курса средней школы, что при изменении температуры давление и удельный вес так называемых идеальных газов удовлетворяют следующему уравнению:

(95.2)

339

где Т — температура газов по шкале Кельвина, R — постоянная для всех газов величина (газовая постоянная),  — молекулярный вес газа. Шкала Кельвина Т связана со шкалой Цельсия t соотно­шением Т=t+273.

Для большинства газов при обычной температуре приближенно справедливо уравнение (95.2), называемое уравнением Клапейрона.

§ 96. Распределение давления в покоящейся жидкости

При формулировке и выводе закона Паскаля мы не учиты­вали веса жидкости (или газа). Теперь оценим влияние веса жид­кости на распределение давления внутри покоящейся несжимае­мой жидкости.

Очевидно, что давление по горизонтали всегда будет одинаково, иначе не было бы равновесия. Отсюда следует, что свободная по­верхность покоящейся жидкости всегда горизонтальна вдали от стенок сосуда. Заметим, что этот вывод справедлив и для неодно­родной жидкости. По вертикали давление будет изменяться, как можно видеть из выражения (94.2); давление возрастает с глуби­ной при переходе от точки С к точке D (см. рис. 273), оно возрастает за счет тяжести жидкости, находящейся в призмочке с вертикаль­ными стенками, имеющей свои основания около точек С и D.

Если жидкость несжимаема, вернее, если сжимаемостью жид­кости можно пренебречь, то удельный вес у не будет зависеть от давления. Тогда вес столбика жидкости равен

4 (96.1)

где S₀ — поперечное сечение призмочки, l — ее длина. Следова­тельно, давление на нижнее основание призмочки возрастет на величину

(96.2)

т. е. давление линейно изменяется с изменением высоты.

Возрастание давления в жидко­сти с глубиной определяет вы­талкивающие силы, действующие на погруженные и плавающие на поверхности жидкости тела (см. § 98).

Распределением давления в жидкости объясняется «гидроста­тический парадокс» с силой давления на дно сосуда (рис. 274). Сила давления на дно сосуда не равна весу жидкости в сосуде, она может быть больше веса жидкости, находящейся в сосуде

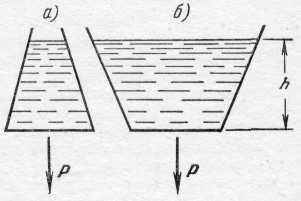
Рис. 274.

340

(рис. 274, а), и меньше (рис. 274, б) вследствие того, что давление на дно зависит только от высоты уровня и удельного веса жидкости, а сила давления на дно равна произведению давления на площадь дна S:

Для измерения разности давлений часто применяются манометры в виде сообщающихся сосудов (рис. 275, а). Очевидно, что жидкость только тогда будет

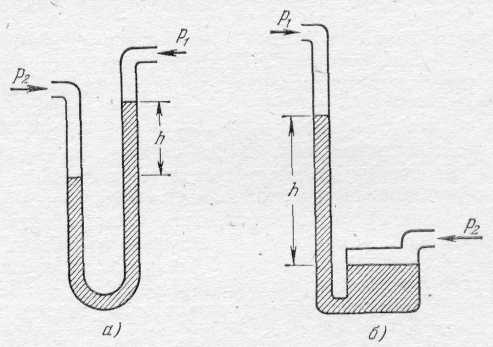
Рис. 275.

в равновесии, когда вследствие разности уровней в сосудах возникает противо­давление h, уравновешивающее разность давлений над жидкостями в сообщаю­щихся сосудах р₂-р₁. Из условий равновесия следует:

где h — разность уровней жидкости в сообщающихся сосудах. (Если трубки сосуда одинаковы, то можно не принимать во внимание силы поверхностного натяжения жидкости.) Обычно при пользовании манометрами этого типа разность давлений измеряют высотой столба той жидкости, которая заполняет манометр. Так, говорят о разности давления в сантиметрах или миллиметрах водяного, спиртового или ртутного столба.

Практически для удобства отсчета пользуются сообщающимися сосудами различного диаметра (рис. 275, б), так как в этом случае можно не считаться с изменением уровня в широком сосуде и вести отсчет только по высоте столба в узенькой трубке ¹). Легко убедиться, что если отношение диаметров сечения сосудов равно 50, то ошибка будет меньше 0,05%.

¹) Конечно, здесь уже нельзя пренебрегать влиянием поверхностного натя­жения. Но если отсчитывать только изменения давления, то постоянная добавка разности давления, возникающая вследствие поверхностного натяжения, не изменит результата.

341