Дифференциальные уравнения движения смт
На основании второго (основного) закона динамики в форме для каждой МТ можно записать:
(=1,
2, ..., n). (1)
Система (1) является системой n дифференциальных уравнений движения СМТ в векторной форме.
Если спроектировать соотношения (1) на оси декартовой системы координат, то получим систему 3n дифференциальных уравнений движения СМТ в координатной форме:
=1,
2, ..., n (2)
11 Центр масс смт. Моменты инерции смт
Пусть
СМТ состоит из n
МТ с массами
,
,.…,
.
Определение: Центром масс СМТ называется геометрическая точка C, радиус-вектор которой определяется выражением:
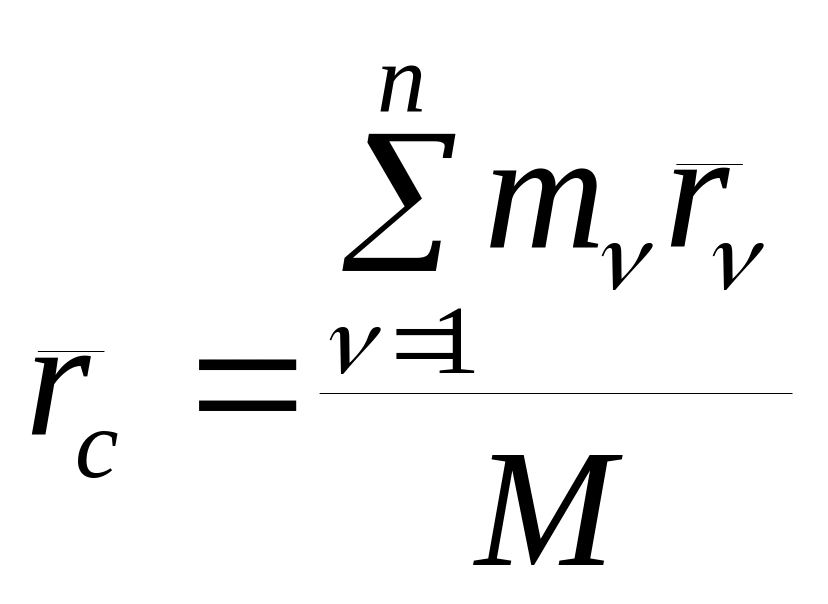, (1)
где М – масса СМТ, которая определяется соотношением:
.
(2)
Спроектировав соотношение (1) на оси декартовой системы координат, получим формулы для координат центра масс СМТ:
.
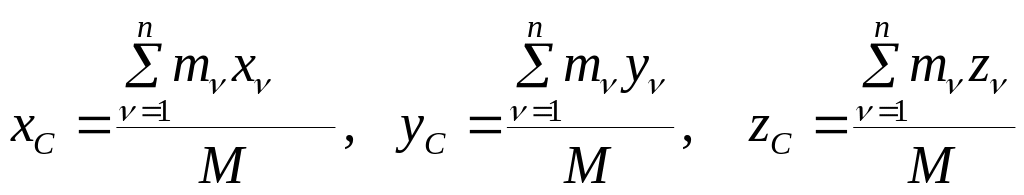Моментом
инерции СМТ относительно точки О
– JO
называется сумма произведений масс МТ
на квадраты их расстояний –
до точки О:
. (3)
Моментом
инерции СМТ относительно оси
(например, оси z)
–
называется
сумма произведений масс МТ на квадраты
их расстояний – h
до оси z:
. (4)
Моментом инерции СМТ относительно плоскости П – JП называется сумма произведений масс МТ на квадраты их расстояний – d до плоскости П:
. (5)
Для того чтобы найти моменты инерции для НМС, необходимо НМС разбить на n элементарных частей, записать формулы (3) – (5) и в них перейти к пределу при n. Тогда получим:
,
,
,
где dm – масса элементарной частицы НМС.
Моменты инерции СМТ относительно начала координат, координатных осей и координатных плоскостей декартовой системы координат (рис) на основании соотношений (3)–(5) можно записать в виде:
.
(6)
(7)
(8)
Из полученных формул следуют свойства вышеназванных моментов инерции:
(9)
В случае сложной конфигурации НМС его момент инерции определяется экспериментально и может быть выражен через радиус инерции. В этом случае момент инерции определяется по формуле:
,
где
– радиус инерции.
12 Теорема о моментах инерции относительно параллельных осей – теорема Штейнера-Гюйгенса
Теорема: Момент инерции СМТ относительно любой оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс, и произведения массы СМТ на квадрат расстояния между осями.
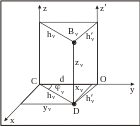
Пусть известен момент инерции СМТ относительно оси Cz, проходящей через ее центр масс С. Найдем момент инерции СМТ относительно оси Оz', параллельной оси z и отстоящей от нее на расстояние d .
Начало декартовой системы координат выберем в центре масс С, ось Сy проведем так, чтобы она пересекала ось Оz'.
Возьмем
произвольную точку В
СМТ массы m
с координатами
x,
y,
z.
Расстояние от этой точки до оси Cz
– h,
а до оси Оz'
–
.
На основании определения момент инерции СМТ относительно оси Оz' имеет вид:
.
Для треугольника СОD из теоремы косинусов следует, что
,
или
,
так как
.
Подставив
в выражение для
,
будем иметь:
.
Так
как
,
и
,
то для получим:
, что
и требовалось доказать.