4 Свободное колебательное движение мт (в среде без сопротивления при отсутствии возмущающей силы)

В этом случае дифференциальное уравнение движения имеет вид:

, (1)

а его решение:

, (2)

где а и  – постоянные интегрирования, которые находятся из начальных условий.

МТ перемещается по закону синуса (или косинуса). Такое движение носит название простого гармонического колебания, график его представлен на рисунке

Скорость этого гармонического колебания МТ будет:

. (3)

Так как , то постоянная а определяет наибольшее отклонение МТ от центра колебаний О и называется амплитудой колебаний МТ. Параметр определяет положение МТ и ее скорость в каждый момент времени и называется фазой колебаний, а постоянная α – начальной фазой.

На основании уравнения (2) можно сделать вывод, что движение МТ является периодическим. Периодом колебаний называется промежуток времени Т_п, в течение которого МТ совершает одно полное колебание, т.е. МТ в момент времени t + T_п должна прийти в то же положение х и иметь ту же скорость , что и в момент времени t:

, .

Наименьшее значение t, при котором выполняются эти условия, определяются равенством , откуда

.

Величина обратная периоду, определяет число колебаний, совершаемых МТ за одну секунду, и ее называют частотой колебаний:

.

Соответственно параметр ω называется круговой частотой колебаний. Необходимо отметить, что частота и период колебаний МТ от начальных условий не зависят.

5 Колебательное движение мт в среде с сопротивлением при отсутствии возмущающей силы

В этом случае дифференциальное уравнение движения в проекции на ось Х примет вид:

, (1)

и решение при малом сопротивлении среды (n < ) в соответствии с формулой

, (2)

где а и  – постоянные интегрирования, которые находятся из начальных условий.

Из уравнения (2) следует, что движение МТ будет колебательным. Эти колебания называют затухающими, так как за счет множителя размахи колебаний будут убывать, стремясь с течением времени к нулю. Период затухающих колебаний

.

Графически затухающие колебания можно иллюстрировать затухающей синусоидой (Рис. 1)

Рис. 1

Чтобы установить закон затухания размахов колебания, отметим, что промежуток времени между двумя последовательными максимальными отклонениями МТ и равен периоду Т_п, т.е. . С учетом этого найдем:

.

Отсюда следует, что наибольшие отклонения МТ убывают с течением времени по закону геометрической прогрессии, знаменатель которой называется декрементом колебаний. Соответственно величина называется логарифмическим декрементом затухания.

В случае большого сопротивления среды (n > ) движение МТ будет неколебательным (апериодическим) затухающим:

,

где – действительные отрицательные числа, а С₁ и С₂ - постоянные интегрирования, которые находятся из начальных условий.

График этого движения МТ в зависимости от величины и знака начального отклонения х₀ и направления начальной скорости имеет форму одной из кривых, изображенных на рисунке (или им симметричных относительно оси абсцисс).

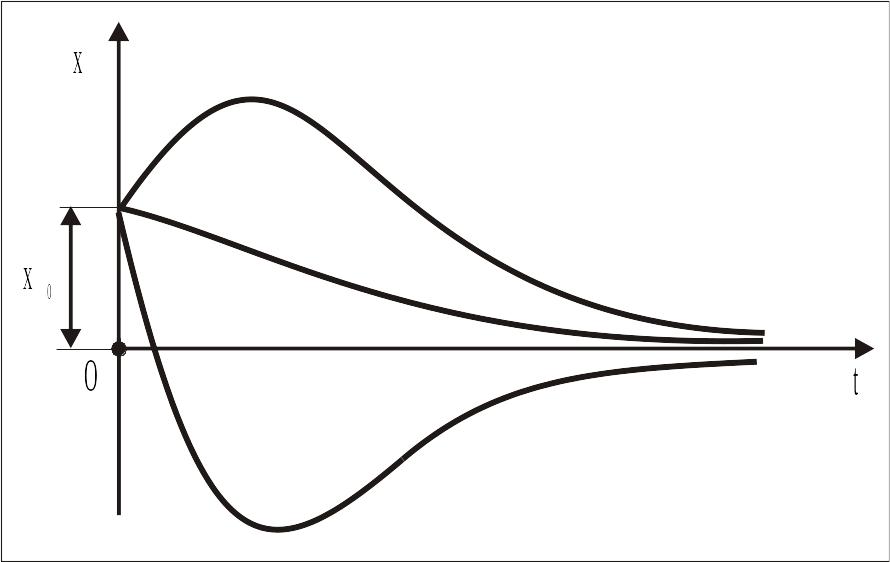
Рис. 2

В предельном случае (n = ) движение МТ также будет неколебательным (апериодическим) затухающим:

,

где С₁ и С₂ – постоянные интегрирования, которые находятся из начальных условий.

Картина движения МТ будет качественно такой же, как показанная на рис. 2.