22Принцип Даламбера для материальной точки и механической системы. Уравнения метода кинетостатики

Основное уравнение динамики точки:

(1)

П еренесем произведение массы на ускорение в правую часть:

Получившееся дополнительное слагаемое имеет размерность силы и принимается

за силу инерции, направленную в сторону противоположную ускорению:

(2)

С введением силы инерции уравнение динамики точки принимает вид уравнения равновесия:

(3)

Принцип Даламбера для материально точки:

Геометрическая сумма приложенных к точке сил и силы инерции этой точки равна нулю.

Для несвободной материально точки под следует понимать не только активные силы, но и реакции связей (в соответствии с аксиомой связей). Сила инерции условно добавляется к действующим на точку силам, образуя взаимно уравновешенную систему сил.

Принцип Даламбера для несвободной механической системы получим, записывая

принцип Даламбера для каждой k-той точки и вводя реакции связей по аксиоме связей:

(4)

Здесь – равнодействующая задаваемых сил, приложенных к точке,

– равнодействующая реакций связей, приложенных к точке, – сила инерции точки.

На практике пользуются следствиями этих уравнений (принципа Даламбера).

Сложим все N уравнений: или

(5)

где – главный вектор задаваемых сил, приложенных к точке,

– главный вектор реакций связей, приложенных к точке, – главный вектор сил инерции точек системы.

Следствие 1: Геометрическая сумма главных векторов задаваемых сил, реакций связи и сил инерции материальных точек равна нулю.

Умножим каждое из N уравнений, выражающее принцип Даламбера системы

на радиус-вектор, проведенный из центра O

.

Теперь сложим все N уравнений: или

, (6)

где – главный момент задаваемых сил относительно центра O,

– главный момент реакций связей относительно центра O,

– главный момент сил инерции точек системы относительно центра O.

Следствие 2: Геометрическая сумма главных моментов задаваемых сил, реакций связи и сил инерции материальных точек относительно любого центра равна нулю.

Уравнения (5,6) называют обычно уравнениями метода кинетостатики.

23.Определение динамических реакций в точках закрепления вращающегося тела

Рассмотрим тело массы М, имеющее две закрепленные точки О и В, которое вращается под действием активных сил вокруг неподвижной оси, проходящей через эти точки (рис. 1).

Рис. 1

Примем точку О за начало неизменно связанной с НМС декартовой системы координат Оxyz, направив ось Oz вдоль оси вращения НМС в сторону точки В. Расстояние между подпятником О и подшипником В обозначим через h. Освободив НМС от связей в точках О и В, приложим к НМС силы реакций связей и , проекции которых на оси координат обозначим соответственно и . Для определения пяти реакций связи воспользуемся принципом Даламбера.

Запишем формулу для ускорения центра масс тела, вращающегося относительно неподвижной оси:

,

где – радиус-вектор центра масс НМС, и – соответственно угловая скорость и ускорение НМС, направленные по оси вращения.

Векторное произведение двух векторов выражается определителем, в первой строке которого расположены единичные вектора , направленные вдоль осей координат, а в двух других строках - проекции на оси координат векторов сомножителей. Представив векторное произведение в виде определителя и учтя при этом, что и , разложим его по элементам первой строки:

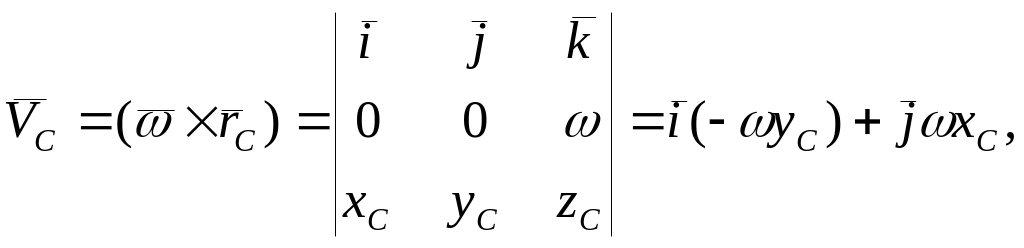(1)

здесь – координаты центра масс НМС.

Используя соотношение (1) и учтя, что , ускорение центра масс можно представить в виде суммы двух определителей:

.

Разложив это соотношение по единичным ортам декартовой системы координат, получим:

. (2)

С учетом соотношения главный вектор сил инерции примет вид:

. (3)

Найдем выражение для главного момента сил инерции. По аналогии с соотношением (2) для ускорения -й точки системы можно записать:

. (4)

Тогда учитывая, что

выражение для главного момента сил инерции может быть представлено с учетом выражения (4) в виде определителя:

,

вычисляя который, имеем:

(5)

С учетом соотношений для центробежных моментов и момента инерции относительно осей:

,

выражение для главного момента сил инерции примет вид:

(6)

Подставляя найденные соотношения в уравнения метода кинетостатики

и проектируя затем полученные соотношения на оси декартовой системы координат, будем иметь систему уравнений для определения динамических реакций , :

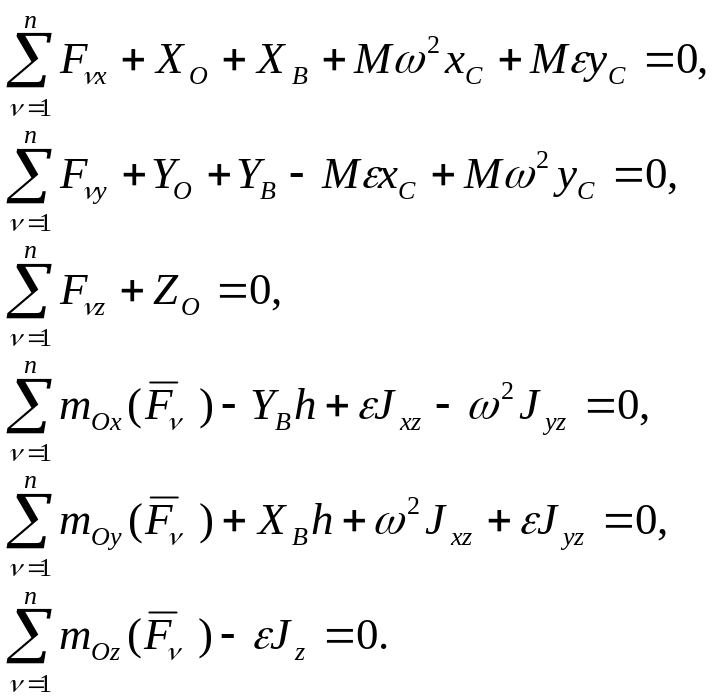(7)

Первые пять уравнений соотношений (7) позволяют определить полные динамические реакции , , шестое уравнение является уравнением вращательного движения НМС вокруг неподвижной оси.

Полные динамические реакции складываются из статических и дополнительных динамических реакций:

, (8)

.

Статические реакции , возникают только вследствие действия задаваемых внешних сил и могут быть определены в предположении, что НМС находится в покое. Полагая в (7) и , получим:

(9)

Дополнительные динамические реакции являются следствием вращательного движения НМС вокруг оси Оz. Подставив соотношение (8) в выражение 7) и учитывая соотношения (9), будем иметь:

(10)

Найдем условия отсутствия дополнительных динамических реакций, для чего в соотношениях (10) положим их равными нулю ( в любом случае вращательного движения НМС вокруг неподвижной оси):

(11) (12)

Системы уравнений (11) и (12) являются системами двух однородных уравнений с двумя неизвестными соответственно х_С, у_С и J_xz и J_yz. Так как главные определители систем не равны нулю:

,

то эти системы удовлетворяют только следующие значения неизвестных:

х_С = 0, у_С = 0, (13)

J_xz = 0, J_yz = 0. (14)

Равенства (13) показывают, что ось вращения z должна проходить через центр масс C НМС, а равенства (14) показывают, что ось вращения z должна совпадать с одной из главных осей инерции НМС в точке О, т. е. ось вращения z будет являться одной из главных, центральных осей инерции НМС.

Таким образом, если ось вращения является одной из главных, центральных осей инерции НМС, то дополнительные динамические реакции отсутствуют, т. е. полные динамические реакции не отличаются от статических, возникающих под действием только задаваемых сил. В этом случае говорят, что вращающаяся НМС динамически уравновешена на оси вращения, а ось вращения называется свободной осью.