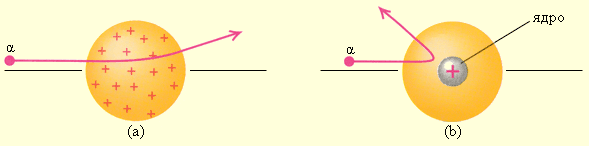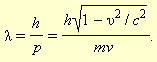Опыт Резерфорда. Ядерная модель атома

Большие успехи в исследовании строения атомов были достигнуты в опытах английского ученого Эрнеста Резерфорда по рассеянию  -частиц при прохождении через тонкие слои вещества. В этих опытах узкий пучок  -частиц, испускаемых радиоактивным веществом, направлялся на тонкую золотую фольгу. За фольгой помещался экран, способный светиться под ударами быстрых частиц. Было обнаружено, что оолынинство  -частиц отклоняется от прямолинейного распространения после прохождения фольги, т. е. рассеивается, а некоторые  -частицы вообще отбрасываются назад. Рассеяние  -частиц Резерфорд объяснил тем, что положительный заряд не распределен равномерно в шаре радиусом 10^-10 м, как предполагали ранее, а сосредоточен в центральной части атома — атомном ядре. При прохождении около ядра  -частица, имеющая положительный заряд, отталкивается от него, а при попадании в ядро — отбрасывается в противоположном направлении. Так ведут себя частицы, имеющие одинаковый заряд, следовательно, существует центральная положительно зараженная часть атома, в которой сосредоточена значительная масса атома. Расчеты показали, что для объяснения опытов нужно принять радиус атомного ядра равным примерно 10^-15 м.

Резерфорд предположил, что атом устроен подобно планетарной системе. Суть модели строения атома по Резерфорду заключается в следующем: в центре атома находится положительно заряженное ядро, в котором сосредоточена вся масса, вокруг ядра по круговым орбитам на больших расстояниях вращаются электроны (как планеты вокруг Солнца). Заряд ядра совпадает с номером химического элемента в таблице Менделеева.

Планетарная модель строения атома по Резерфорду не смогла объяснить ряд известных фактов: электрон, имеющий заряд> должен за счет кулоновских сил притяжения упасть на ядро, а атом — это устойчивая система; при движении по круговой орбите, приближаясь к ядру, электрон в атоме должен излучать электромагнитные волны всевозможных частот, т. е. излучаемый свет должен иметь непрерывный спектр, на практике же получается иное: электроны атомов излучают свет, имеющий линейчатый спектр. Разрешить противоречия планетарной ядерной модели строения атома первым попытался датский физик Нильс Бор.

Рисунок 6.1.1. Модель атома Дж. Томсона

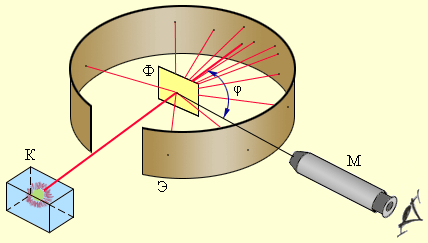
Рисунок 6.1.2. Схема опыта Резерфорда по рассеянию α-частиц. K – свинцовый контейнер с радиоактивным веществом, Э – экран, покрытый сернистым цинком, Ф – золотая фольга, M – микроскоп

Рисунок 6.1.3. Рассеяние α-частицы в атоме Томсона (a) и в атоме Резерфорда (b)
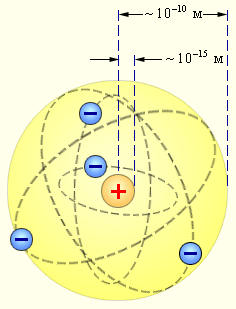
Рисунок 6.1.4. Планетарная модель атома Резерфорда. Показаны круговые орбиты четырех электронов

18+ Атом водорода по Бору. Опыты Франка и Герца.

В основу своей теории Бор положил два постулата. Первый постулат: атомная система может находиться только в особых стационарных или квантовых состояниях, каждому из которых соответствует своя энергия; в стационарном состоянии атом не излучает.

Это означает, что электрон (например, в атоме водорода) может находиться на нескольких вполне определенных орбитах. Каждой орбите электрона соответствует вполне определенная энергия.

Второй постулат: при переходе из одного стационарного состояния в другое испускается или погл-щается квант электромагнитного излучения. Энергия фотона равна разности энергий атома в двух состояниях:  ;  , где   — постоянная Планка.

При переходе электрона с ближней орбиты на более удаленную атомная система поглощает квант энергии. При переходе с более удаленной орбиты электрона на ближнюю орбиту по отношению к ядру и томная система излучает квант энергии. Теория Бора позволила объяснить существование линейчатых спектров.

Бо́ровская моде́ль а́тома (Моде́ль Бо́ра) — полуклассическая модель атома, предложеннаяНильсом Бором в 1913 г. За основу он взял планетарную модель атома, выдвинутуюРезерфордом. Однако, с точки зрения классической электродинамики, электрон в модели Резерфорда, двигаясь вокруг ядра, должен был бы излучать непрерывно, и очень быстро, потеряв энергию, упасть на ядро. Чтобы преодолеть эту проблему Бор ввел допущение, суть которого заключается в том, что электроны в атоме могут двигаться только по определенным (стационарным) орбитам, находясь на которых они не излучают, а излучение или поглощение происходит только в момент перехода с одной орбиты на другую. Причем стационарными являются лишь те орбиты, при движении по которым момент количества движения электрона равен целому числу постоянных Планка^[1]:  .

Используя это допущение и законы классической механики, а именно равенство силы притяжения электрона со стороны ядра и центробежной силы, действующей на вращающийся электрон, он получил следующие значения для радиуса стационарной орбиты R_n и энергии E_nнаходящегося на этой орбите электрона:

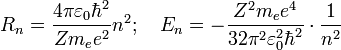
Здесь m_e — масса электрона, Z — количество протонов в ядре,   — электрическая постоянная, e — заряд электрона.

Именно такое выражение для энергии можно получить, применяя чисто квантовомеханическийподход, решая задачу о движении электрона в центральном кулоновском поле.

Радиус первой орбиты в атоме водорода R₀=5,2917720859(36)×10⁻¹¹ м^[2], ныне называется боровским радиусом, либо атомной единицей длины и широко используется в современной физике. Энергия первой орбиты E₀=-13.6 эВ представляет собой энергию ионизации атома водорода.

Опыт Франка — Герца — опыт, явившийся экспериментальным доказательством дискретности внутренней энергии атома. Поставлен в 1913 Дж. Франком и Г. Герцем.

На рисунке приведена схема опыта. К катоду К и сетке C1 электровакуумной трубки, наполненной парами Hg (ртути), прикладывается разность потенциалов V, ускоряющая электроны, и снимается зависимость силы тока I от V. К сетке C2 и аноду А прикладывается замедляющая разность потенциалов. Ускоренные в области I электроны испытывают соударения с атомами Hg в области II. Если энергия электронов после соударения достаточна для преодоления замедляющего потенциала в области III, то они попадут на анод. Следовательно, показания гальванометра Г зависят от потери электронами энергии при ударе.

В опыте наблюдался монотонный рост I при увеличении ускоряющего потенциала вплоть до 4,9 в, то есть электроны с энергией Е < 4,9 эв испытывали упругие соударения с атомами Hg и внутренняя энергия атомов не менялась. При значении V = 4,9 в (и кратных ему значениях 9,8 в, 14,7 в) появлялись резкие спады тока. Это определённым образом указывало на то, что при этих значениях V соударения электронов с атомами носят неупругий характер, то есть энергия электронов достаточна для возбуждения атомов Hg. При кратных 4,9 эв значениях энергии электроны могут испытывать неупругие столкновения несколько раз.

Таким образом, опыт Франка — Герца показал, что спектр поглощаемой атомом энергии не непрерывен, а дискретен, минимальная порция (квант электро-магнитного поля), которую может поглотить атом Hg, равна 4,9 эВ. Значение длины волны λ = 253,7 нм свечения паров Hg, возникавшее при V > 4,9 В, оказалось в соответствии со вторым постулатом Бора

,где E₀ и E₁ — энергии основного и возбужденного уровней энергии. В опыте Франка — Герца, E₀ — E₁ = 4,9 эв.

Артур Комптон, повторив (1922—1923) опыт Франка — Герца, обнаружил, что при V > 4,9 в пары Hg начинают испускать свет с частотой n = DE/h, где DE = 4,9 эв (h — постоянная Планка). Таким образом, возбуждённые электронным ударом атомы Hg испускают фотон с энергией 4,9 эв и возвращаются в основное состояние.

В 1925 г. Густав Герц и Джеймс Франк были награждены нобелевской премией за открытие законов соударения электрона с атомом.

19+ Корпускулярно-волновой дуализм вещества. Волны де-Бройля. Волновые свойства микрочастиц.

Корпускулярно-волновой дуализм — физический принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства. Был введён при разработке квантовой механики для объяснения явлений, наблюдаемых в микромире.

В частности, свет — это и корпускулы (фотоны), и электромагнитные волны. Свет демонстрирует свойства волны в явлениях дифракции и интерференции при масштабах, сравнимых с длиной световой волны. Например,одиночные фотоны, проходящие через двойную щель, создают на экране интерференционную картину, определяемую уравнениями Максвелла.^[1]. Тем не менее, эксперимент показывает, что фотон не есть короткий импульс электромагнитного излучения, например, он не может быть разделён на несколько пучков оптическими делителями лучей. Корпускулярные свойства света проявляются при фотоэффектеи в эффекте Комптона. Фотон ведет себя и как частица, которая излучается или поглощается целиком объектами, размеры которых много меньше его длины волны (например, атомными ядрами), или вообще могут считаться точечными (например, электрон).

Во́лны де Бро́йля — волны, связанные с любой микрочастицей и отражающие их квантовую природу.

Для частиц не очень высокой энергии, движущихся со скоростью   (скорости света), импульс равен   (где   — масса частицы), и  . Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость. Например, частице с массой в 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с   м, что лежит за пределами доступной наблюдению области. Поэтому волновые свойства несущественны в механике макроскопических тел. Для электронов же с энергиями от 1 эВ до 10 000 эВ длина волны де Бройля лежит в пределах от ~ 1 нм до 10^-2 нм, то есть в интервале длин волн рентгеновского излучения. Поэтому волновые свойства электронов должны проявляться, например, при их рассеянии на тех же кристаллах, на которых наблюдается дифракция рентгеновских лучей.

Первое подтверждение гипотезы де Бройля было получено в 1927 году в опытах американских физиков К. Дэвиссона и Л. Джермера. Пучокэлектронов ускорялся в электрическом поле с разностью потенциалов 100—150 В (энергия таких электронов 100—150 эВ, что соответствует  нм) и падал на кристалл никеля, играющий роль пространственной дифракционной решётки. Было установлено, что электроны дифрагируют на кристалле, причём именно так, как должно быть для волн, длина которых определяется соотношением де Бройля.

Подтвержденная на опыте идея де Бройля о двойственной природе микрочастиц — корпускулярно-волновом дуализме — принципиально изменила представления об облике микромира. Поскольку всем микрообъектам (по традиции за ними сохраняется термин «частица») присущи и корпускулярные, и волновые свойства, то, очевидно, любую из этих «частиц» нельзя считать ни частицей, ни волной в классическом понимании. Возникла потребность в такой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории — волновой, или квантовой, механики — и легла концепция де Бройля. Это отражается даже в названии «волновая функция» для величины, описывающей в этой теории состояние системы. Квадрат модуля волновой функции определяет вероятность состояния системы, и поэтому о волнах де Бройля часто говорят как о волнах вероятности (точнее, амплитуд вероятности). Для свободной частицы с точно заданным импульсом p (и энергией  ), движущейся вдоль оси x, волновая функция имеет вид:

где   — время,  .

В этом случае  , то есть вероятность обнаружить частицу в любой точке одинакова.

Французский физик Л. де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами.

Согласно де Бройлю, с каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота ν и длина волны λ.

Корпускулярные и волновые характеристики микрообъектов связаны такими же количественными соотношениями, как и у фотона: 

Гипотеза де Бройля постулировала эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой m. Любой частице, обладающей импульсом, сопоставлялся волновой процесс с длиной волны λ = h / p. Для частиц, имеющих массу, 

В нерелятивистском приближении (υ << c) 

20+ Принцип неопределённости Гейзенберга.

Принцип неопределённости Гейзенбе́рга (или Га́йзенберга) в квантовой механике — фундаментальное неравенство (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих квантовую систему физических наблюдаемых, описываемых некоммутирующимиоператорами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Соотношение неопределенностей задает нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых. 

Если приготовлены несколько идентичных копий системы в данном состоянии, то измеренные значения координаты и импульса будут подчиняться определённому распределению вероятности — это фундаментальный постулат квантовой механики. Измеряя величину среднеквадратического отклонения Δx координаты и среднеквадратического отклонения Δp импульса, мы найдем что:

,

где   — приведённая постоянная Планка. В некоторых случаях «неопределённость» переменной определяется как наименьшая ширина диапазона, который содержит 50 % значений, что, в случае нормального распределения переменных, приводит для произведения неопределённостей к большей нижней границе  . Отметьте, что это неравенство даёт несколько возможностей — состояние может быть таким, что x может быть измерен с высокой точностью, но тогда p будет известен только приблизительно, или наоборот p может быть определён точно, в то время как x — нет. Во всех же других состояниях, и x и p могут быть измерены с «разумной» (но не произвольно высокой) точностью.

В повседневной жизни мы обычно не наблюдаем неопределённость потому, что значение   чрезвычайно мало.

21+ Волновая функция. Уравнение Шредингера.

Волновая функция (функция состояния, пси-функция) — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния квантовомеханической системы. В широком смысле — то же, что и вектор состояния.

Квадрат модуля волновой функции называется амплитудой вероятности, что связано с копенгагенской интерпретацией квантовой механики: плотность вероятности нахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния.