10) Потенциальная энергия деформации стержня в общем случае его нагружения

Потенциальная энергия деформации при растяжении, кручении и изгибе была рассмотрена в предыдущих лекциях. При изгибе мы не учитываем энергию, возникшую за счёт сдвига.

В общем случае сопротивления бруса деформированию при нагружении в его поперечных сечениях возникают шесть внутренних силовых факторов:

Для бруса длиной из линейно-упругого материала потенциальная энергия определяется формулой

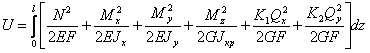, (1)

где коэффициенты зависят от формы поперечного сечения. Например, для прямоугольного сечения , для круглого - для тонкостенной трубки

Если стержневая система состоит из нескольких элементов, то необходимо произвести суммирование энергий по числу этих элементов. Энергия растяжения и сдвига, как правило, меньше энергий изгиба и кручения. Вместе с тем возможны случаи (например, внецентренное сжатие), когда энергия растяжения и изгиба одного порядка. Энергия от сдвига в (1), сопровождаемая возникновением перерезывающих сил, может быть определена следующим образом: удельная потенциальная энергия чистого сдвига Следовательно,

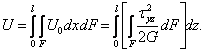
Используя формулу Журавского для касательного напряжения, найдём:

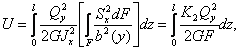
где обозначено

формула Кастилиано — одна из осн. теорем механики линейно деформируемого тела, находящегося иод действием системы независимых друг от друга внешних сил. Сущность теоремы Кастильяно состоит в том, что частная производная от потенциальной энергии тела по одной из приложенных сил равна перемещению точки приложения этой силы по направлению последней.

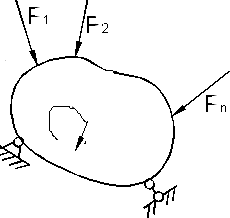
Пусть на закрепленное тело действует система сил. Пусть dFn при этом на малую величину измениться и потенциал. Энергия деформации.

U1=U+dU

dU= dU/dFn*dFn

U1=U+dU/ dFn*dFn (1) она вызывает бескон.мал. перемещение dFn dбn

dW1= dFn*dбn (2)

приложим всю систему сил

W2=U+dFn*бn

W= dFn*dбn+U+ dFn*бn (3)

U1=W

Учит 1 и2

U+ dU/ dFn*dFn= dFn*dбn+U+ dFn*бn

dU/ dFn= dбn+бn

dU/ dFn= бn – Теорема Кастильяно

Теорема Кастильяно. – перемещение точки приложения обобщенной силы по направлению ее действия равно частной производной от потенциальной энергии по этой силе. Пренебрегая влиянием на перемещение осевых и поперечных сил, имеем потенциальную энергию: , откуда .

Применяя теорему Кастильяно к развернутому выражению потенц. энергии в общем виде через внутр. силы (через М, Q, N — для стержневых систем и через а и т — для сплошных тел), можно обосновать метод Мора — Максвелла для вычисления перемещений линейно деформируемых стержневых систем или обобщение этого метода иа сплошные тела; более общее доказательство, предусматривающее также перемещения от изменения темп-ры и т.п., вытекает из принципа возможных перемещений.

В литературе теорема Кастильяно иногда используется для непосредств. вычисления перемещений с составлением развернутого выражения потенц. энергии в условиях частной задачи и его дифференцированием. Этот прием менее эффективен, чем метод Мора— Максвелла, и является устаревшим.

У

ниверсальный метод определения перемещений (линейных и углов поворота) – метод Мора. К системе прикладывают единичную обобщенную силу в точке, для которой ищется обобщенное перемещение. Если определяется прогиб, то единичная сила представляет собой безразмерную сосредоточенную силу, если определяется угол поворота, то – безразмерный единичный момент. В случае пространственной системы действуют шесть компонентов внутренних усилий. Обобщенное перемещение определяется формулой (формула или интеграл Мора):

Черта над М, Q и N указывает на то, что эти внутренние усилия вызваны действием единичной силы. Для вычисления входящих в формулу интегралов надо перемножить эпюры соответствующих усилий.