
- •1.Энергосистема и её структура
- •2.Классификация электрических сетей
- •3.Основные элементы воздушных линий
- •4. Провода воздушных линий
- •5.Опоры воздушных линий и их основания
- •6. Изоляторы и линейная арматура вл
- •7. Кабельные линии электропередач. Общая характеристика.
- •8. Кабельные линии 1-35 кВ
- •9. Кабельная арматура
- •10. Режимы нейтралей электрических сетей. Эс наприжением до 1 кВ (вода …)
- •11.Сети с незаземленной (изолированной) нейтралью
- •12.Сети с компенсированными ( резонансно - заземленными) нейтралями
- •13. Сети с эффективно и глухо заземленными нейтралями
- •14. Общая характеристика схем замещения воздушных и кабельных линий электропередач
- •16. Воздушная лэп с расщепленными фазами
- •17. Моделирование протяженных линий
- •Параметры и схема замещения двухобмоточногоо трансформатора
- •Параметры и схема замещения трехобмоточного трансформатора
- •Параметры и схема замещения автотрансформатора
- •Параметры и схема замещения трансформатора расщ. Обмотками
- •22.Годовые графики нагрузок
- •23Статические характеристики электрических нагрузок
- •24. Моделирование нагрузок постоянным по модулю и фазе током
- •25. Задание нагрузки неизменной мощности Нагрузка задается постоянной по величине мощностью
- •При расчетах установившихся режимов питающих и иногда распределительных сетей высокого напряжения (см. Рис. 2.17,б).
- •27. Общая характеристика задачи расчета и анализа установившихся режимов электрических сетей
- •45 Расчет установившегося режима разомкнутой электрической сети
- •37.Расчет сети методом уравнений контурных токов.
- •38. Расчет сети методом уравнений контурных мощностей.
- •39. Методы расчета и анализа потерь электроэнергии. Метод характерных суточных режимов.
- •40.Определение потерь электроэнергии методом средних нагрузок.
- •41. Определение потерь электроэнергии методом среднеквадратичных параметров режима
- •42. Определение потерь электроэнергии методом времени наибольших потерь.
- •43. Определение потерь электроэнергии методом раздельрого времени наибольших потерь.
- •44. Определение потерь электроэнергии методом эквивалентного сопротивления.
- •45. Подходы к регулированию напряжения в системообразующей эс
- •46. Принципы регулирования напряжения в центрах питания распределительных эс.
- •48. Регулирование напряжения изменением потоков реактивной мощности.
- •50. Выбор конфигурации и номинального напряжения.
- •51. Выбор проводников по условиям экономичности.
- •52. Выбор проводников лэп по допустимой потере напряжения.
- •53. Выбор проводников лэп по условию нагрева.
- •54. Учет технических ограничений при выборе проводов вл и жил кл.
- •55. Пути повышения пропускной способности лэп и эс.
Параметры и схема замещения двухобмоточногоо трансформатора
Двухобмоточный трансформатор (рис. 2.4, а) можно представить в виде Г-образной схемы замещения

Рис. 2.4. Двухобмоточный трансформатор
а-условное обозначение; б-Г-образная схема замещения; в-упрощенная схема замещения
2.4, б).
Продольная
часть схемы замещения содержит
 и
и
 -активное
и реактивное сопротивления трансформатора.
Эти сопротивления равны сумме
соответственно активных
и реактивных сопротивлений первичной
и приведенной
к ней вторичной обмоток. В такой схеме
замещения отсутствует трансформация,
т. е.
отсутствует идеальный трансформатор,
но сопротивление
вторичной обмотки приводится к
первичной. При этом приведении
сопротивление вторичной обмотки
умножается на квадрат коэффициента
трансформации. Если сети, связанные
трансформатором, рассматриваются
совместно, причем параметры сетей не
приводятся к одному базисному напряжению,
то в схеме замещения трансформатора
учитывается идеальный транс-форматор
(см. §3.8,3.9).
-активное
и реактивное сопротивления трансформатора.
Эти сопротивления равны сумме
соответственно активных
и реактивных сопротивлений первичной
и приведенной
к ней вторичной обмоток. В такой схеме
замещения отсутствует трансформация,
т. е.
отсутствует идеальный трансформатор,
но сопротивление
вторичной обмотки приводится к
первичной. При этом приведении
сопротивление вторичной обмотки
умножается на квадрат коэффициента
трансформации. Если сети, связанные
трансформатором, рассматриваются
совместно, причем параметры сетей не
приводятся к одному базисному напряжению,
то в схеме замещения трансформатора
учитывается идеальный транс-форматор
(см. §3.8,3.9).
Поперечная
ветвь схемы (ветвь намагничивания)
состоит из активной и реактивной
проводимостей
 и
и
 .
Активная проводимость соответствует
потерям активной мощности в стали
трансформатора от тока намагничивания
.
Активная проводимость соответствует
потерям активной мощности в стали
трансформатора от тока намагничивания
 (рис. 2.4, б).
Реактивная проводимость определяется
магнитным потоком взаимоиндукции в
обмотках трансформатора.
(рис. 2.4, б).
Реактивная проводимость определяется
магнитным потоком взаимоиндукции в
обмотках трансформатора.
В
расчетах электрических сетей двухобмоточные
трансформаторы при
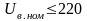 кВ представляют упрощенной схемой
замещения (рис. 2.4, в).
В этой схеме вместо ветви намагничивания
учитываются в виде дополнительной
нагрузки потери мощности в стали
трансформатора или потери холостого
хода
кВ представляют упрощенной схемой
замещения (рис. 2.4, в).
В этой схеме вместо ветви намагничивания
учитываются в виде дополнительной
нагрузки потери мощности в стали
трансформатора или потери холостого
хода
 .
.
Проводимости
ветви намагничивания определяются
результатами опыта холостого хода
(XX). В этом опыте размыкается вторичная
обмотка, а к первичной подводится
номинальное напряжение. Ток в продольной
части схемы замещения равен нулю, а к
поперечной приложено
 (рис.
2.5, а).
Трансформатор потребляет в этом режиме
только мощность, равную потерям холостого
хода, т. е. (рис.
2.5, б)
(рис.
2.5, а).
Трансформатор потребляет в этом режиме
только мощность, равную потерям холостого
хода, т. е. (рис.
2.5, б)
 .
.
Проводимости, См, определяются следующими выражениями:
 ,
(2.9)
,
(2.9)
 ,
(2.10)
,
(2.10)
где напряжения выражены в киловольтах, а мощности в мегаваттах и мегаварах.
Потери
активной мощности в стали определяются
в основном напряжением и приближенно
предполагаются независящими от тока и
мощности нагрузки ( и
и
 ).
В схеме на рис. 2.4, б
).
В схеме на рис. 2.4, б
 постоянна и равна каталожному значению.
Ток намагничивания в трансформаторе
имеет очень
маленькую активную
составляющую:
постоянна и равна каталожному значению.
Ток намагничивания в трансформаторе
имеет очень
маленькую активную
составляющую:
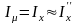 ,
,
где
 -
реактивная составляющая
-
реактивная составляющая
 .Поэтому
.Поэтому

 (2.11)
(2.11)
Отметим,
что
намного меньше, чем
 ,
и полная
мощность трансформатора в
режиме холостого хода
,
и полная
мощность трансформатора в
режиме холостого хода
 приближенно
равна намагничивающей мощности
.
приближенно
равна намагничивающей мощности
.
С учетом (2.11) проводимость определяется так:
 (2.
10а)
(2.
10а)
Сопротивления
трансформатора
и
определяются по результатам опыта
короткого замыкания
(КЗ). В этом опыте замыкается накоротко
вторичная обмотка, а к первичной
обмотке подводится
такое напряжение,
при котором в обеих
обмотках трансформатора
токи равны номинальному.
Это напряжение и
называется напряжением короткого
замыкания
 (рис. 2.5,6
и г).
Потери в стали в опыте
короткого замыкания
(рис. 2.5,6
и г).
Потери в стали в опыте
короткого замыкания
 очень малы, так как
намного меньше
.
Поэтому приближенно
считают, что все потери мощности в опыте
КЗ
очень малы, так как
намного меньше
.
Поэтому приближенно
считают, что все потери мощности в опыте
КЗ
 идут на нагрев обмоток трансформатора,
т. е.
идут на нагрев обмоток трансформатора,
т. е.
 (2.12)
(2.12)
и
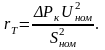 (2.13)
(2.13)
В
современных мощных трансформаторах
«
и

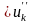 .
Из опыта КЗ (рис.2.5, в)
.
Из опыта КЗ (рис.2.5, в)

Умножая последнее выражение на , после преобразований получим

В (2.13), (2.14) сопротивления получаются в Омах при подстановке напряжений в киловольтах, а мощностей-в мегавольт-амперах и в мегаваттах.
Потери активной мощности в зависят от тока и мощности нагрузки и . Эти потери равны

Если
подставить в последнее выражение
из (2.13)
и учесть, что
 ,
то получим
,
то получим
 .
(2.15)
.
(2.15)
Потери реактивной мощности в аналогично (2.15) определяются так:
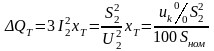 (2.
16)
(2.
16)
Для трансформатора, через который проходят ток нагрузки и мощность , потери мощности с учетом (2.11), 2.15) и (2.16) равны
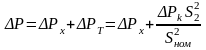 ,
(2.
17)
,
(2.
17)
 .
(2.18)
.
(2.18)
Если
на подстанции с суммарной нагрузкой
работают параллельно k
одинаковых трансформаторов, то их
эквивалентные
сопротивления в k
раз меньше и равны
 ,
,
 ,а
проводимости в k
раз больше, т.е. равны
,а
проводимости в k
раз больше, т.е. равны
 Если
учесть это в выражениях
(2.9), (2.11), (2.15), (2.16), то
получим следующие выражения для потерь
мощности:
Если
учесть это в выражениях
(2.9), (2.11), (2.15), (2.16), то
получим следующие выражения для потерь
мощности:
 ,
(2.19)
,
(2.19)
 ,
(2.20)
,
(2.20)
