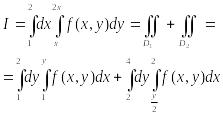Вопрос6.
Определение двойного интеграла.
Основные сведения из теории
Пусть
в ограниченной замкнутой области D
плоскости Оху
задана непрерывная функция z=f(x,y)
(не обязательно положительная). Разобьём
область D
на n
частей D1,
D2,
… Dn
с площадями
![]() и диаметрами d1,
d2,
… dn.
Выберем внутри каждой области Di
произвольную точку Mi(xi,yi)
и составим сумму:
и диаметрами d1,
d2,
… dn.
Выберем внутри каждой области Di
произвольную точку Mi(xi,yi)
и составим сумму:
![]() .
(1)
.
(1)
Сумма
(1) называется n-й
интегральной суммой функции f(x,y),
соответствующей данному разбиению
области D
и данному выбору точек Мi.
Пусть
![]() .
.
Конечный предел, если он существует, n-й интегральной суммы (1), когда наибольший из диаметров частичных областей стремиться к нулю, называется двойным интегралом от функции f(x,y) по области D .
Обозначается:![]() ,
(2)
,
(2)
D – область интегрирования.
Различают два основных вида области интегрирования.
1.
Область интегрирования D
ограничена слева и справа прямыми x=a
и x=b
(a<b),
а снизу и сверху – непрерывными кривыми
![]() и
и
![]() ,
,
![]() ,
каждая из которых пересекается
вертикальной прямой только в одной
точке
,
каждая из которых пересекается
вертикальной прямой только в одной
точке
(рис 12.). Такая область называется правильной по х.
Для такой области интеграл вычисляется по формуле
![]() (3)
(3)
причем сначала вычисляется внутренний интеграл
![]() ,
,
в котором x считается постоянным. Далее, полученную функцию от x интегрируем по промежутку от a до b.
2.
Область интегрирования D
– ограничена снизу и сверху прямыми
y
= c
и y
= d
(c<d),
а слева и справа - непрерывными кривыми
![]()
![]() ,
каждая из которых пересекается
горизонтальной прямой только в одной
точке (рис 13.). Такая область называется
правильной по у.
,
каждая из которых пересекается
горизонтальной прямой только в одной
точке (рис 13.). Такая область называется
правильной по у.
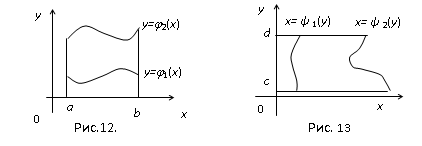
В этом случае двойной интеграл вычисляется по формуле
![]() (4)
(4)
причем сначала вычисляется внутренний интеграл, в котором у считается постоянным.
Правые части формул (3) и (4) называются двукратными интегралами.
Если область интегрирования правильная, двойной интеграл не зависит от порядка интегрирования.
Замечание 1. Двойной интеграл – число, поэтому пределы во внешнем интеграле всегда постоянны.
Замечание 2. Если область интегрирования – прямоугольник, со сторонами, параллельными осям координат, то пределы интегрирования постоянны как во внешнем, так и во внутреннем интеграле:
![]()
Замечание
3. Формула
(3) получена для
![]() ,
исходя из геометрического смысла
двойного интеграла. Оказывается, что
она справедлива для любой
непрерывной функции в области
,
исходя из геометрического смысла
двойного интеграла. Оказывается, что
она справедлива для любой
непрерывной функции в области
![]() .
.
Пример
1. Вычислить
двойной интеграл![]() ,
где D
– прямоугольник:
,
где D
– прямоугольник:
![]()
 Пример
2.
Вычислить двойной интеграл:
Пример
2.
Вычислить двойной интеграл:
![]()
где
D
– треугольник
![]()
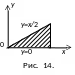
![]()
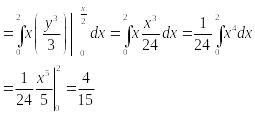
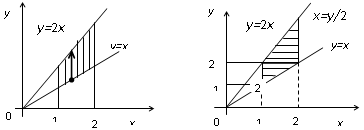
Пример 3. Поменять порядок интегрирования:
![]() ,
где D:
x=1,
x=2,
y=x;
y=2x.
,
где D:
x=1,
x=2,
y=x;
y=2x.