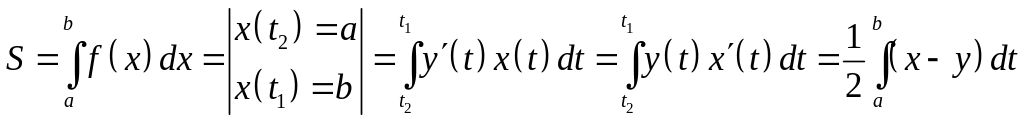1. Задача, о площади криволинейной трапеции приводящая к понятию определенного интеграла.

Криволинейная трапеция – плоская фигура, ограниченная линиями . При этом: непрерывная на .

Разобьем на n частей точками x₁, x₂, … , x_n:

, x₀ = a, x_n = b.

Проведя вертикальные линии из каждой точки . Получим n криволинейных трапеций. Рассмотрим отрезок . Выберем точку . Значение функции в этой точке обозначим за f_i. построим прямоугольник с основанием и высотой f_i.

2. Классы интегрируемых функций.

Теорема 1: Если функция непрерывна на отрезке, то она интегрируема на этом отрезке.

Теорема 2: Если функция ограничена на отрезке и имеет на нём лишь конечное число точек разрыва, то она интегрируема на этом отрезке.

Теорема 3: Если функция монотонна и ограничена на отрезке, то она интегрируема на этом отрезке.

3. Теорема об определенном интеграле с переменным верхним пределом

Теорема:

Определенный интеграл с переменным верхним пределом от функции f(x), непрерывной на [a; b] является первообразной для подынтегральной функции.

Доказательство:

Возьмем и зададим приращение , так, что

Следствие:

У каждой непрерывной функции есть первообразная.

4. Теорема Лейбница – Ньютона.

Теорема:

Если F(x) – какая-то первообразная для f(x), то справедлива формула:

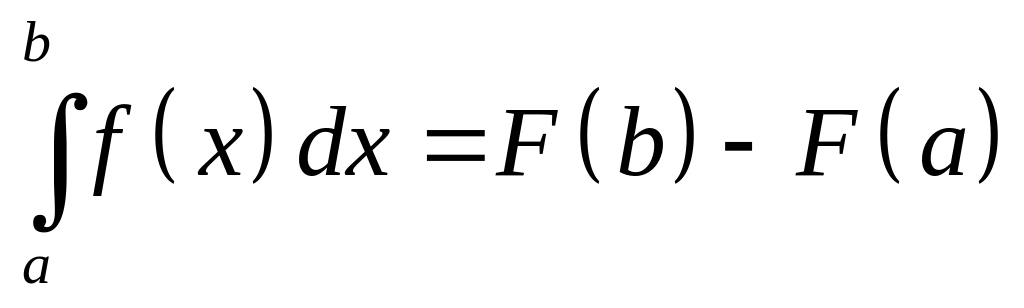
Доказательство:

Пусть F(x) – первообразная для f(x).

По теореме об определенном интеграле с переменным верхним пределом (Определенный интеграл с переменным верхним пределом от функции f(x), непрерывной на [a; b] является первообразной для подынтегральной функции):

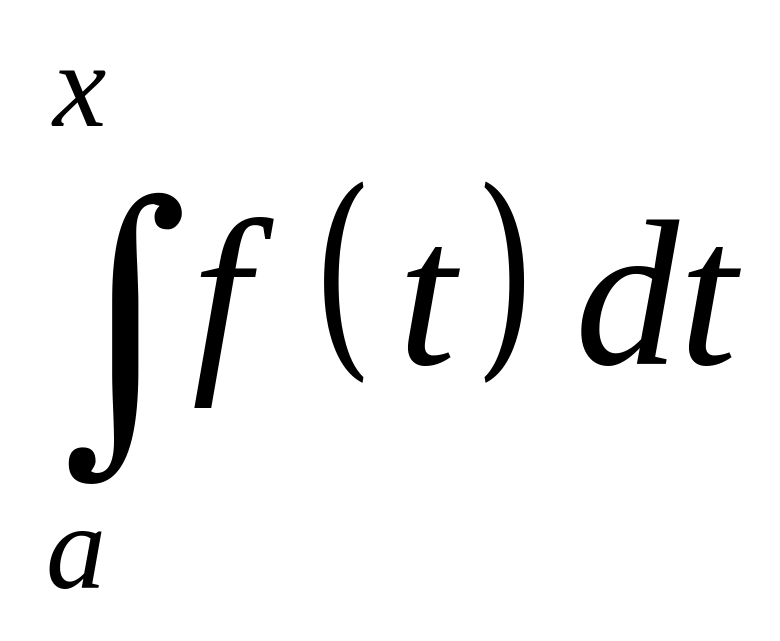– тоже первообразная для f(x).

Две первообразные для f(x) отличаются на C = const. Определим C:

Пусть x = a:

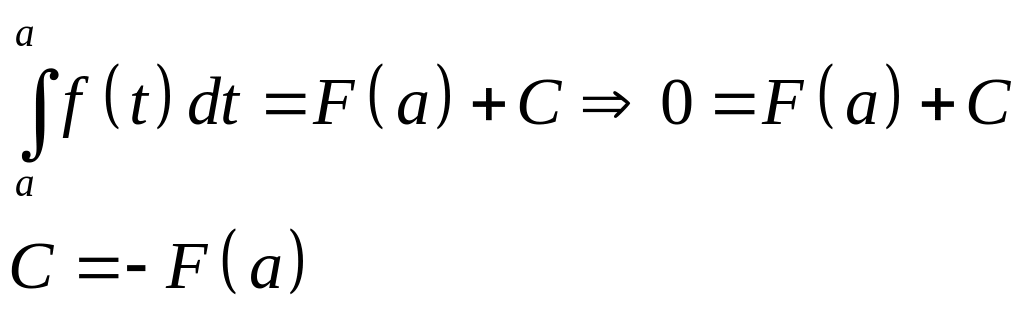
Пусть x = b:

5. Теорема об интегрировании по частям

Теорема:

Пусть функции u(x) и v(x) имеют непрерывные производные на [a; b]. Тогда:

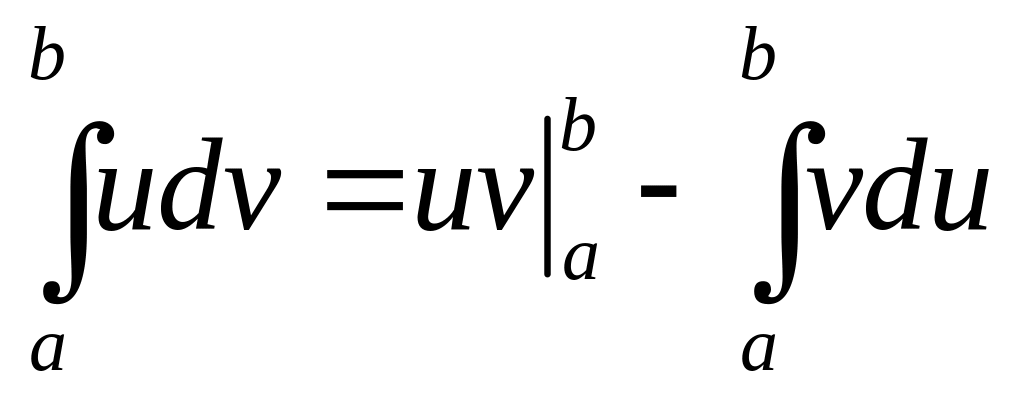
Доказательство:

(uv)’ = u’v + uv’ => uv – первообразная от (u’v+uv’)

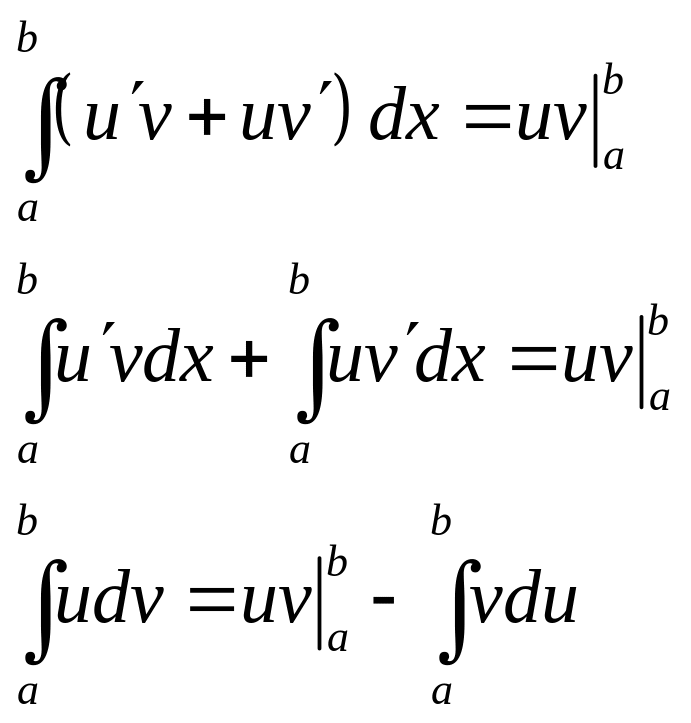
6. Теорема о замене переменной в определенном интеграле

Теорема:

Пусть функция f(x) – непрерывная на [a; b] и функция x = φ(x) – непрерывно дифференцируема на [t₁; t₂], причем φ: [t₁;t₂]→[a; b], и φ(t₁) = a, φ(t₂) = b. Тогда:

Доказательство:

Пусть F(x) – первообразная для f(x) на [a; b]. Тогда:

7. Вывод формулы вычисления площади плоской фигуры (в декартовой системе координат)

Плоская фигура – любое ограниченное множество точек плоскости. Если плоская фигура ограничена:

1. Графиком функции f(x), определенной и непрерывной на отрезке [a; b], f(x) ≥ 0 для всех x из отрезка [a; b], x = a, x = b, y = 0

Тогда разобьем на n частей точками x₁, x₂, … , x_n:

, x₀ = a, x_n = b.

Проведя вертикальные линии из каждой точки . Получим n криволинейных трапеций. Рассмотрим отрезок . Выберем точку . Значение функции в этой точке обозначим за f_i. построим прямоугольник с основанием и высотой f_i.

2. Графиком функции f(x), определенной и непрерывной на отрезке [a; b], f(x) ≤ 0 для всех x из отрезка [a; b], x = a, x = b, y = 0

7. Продолжение истории =))

3. Графиком функции f(x), определенной и непрерывной на отрезке [a; b], x = a, x = b, y = 0

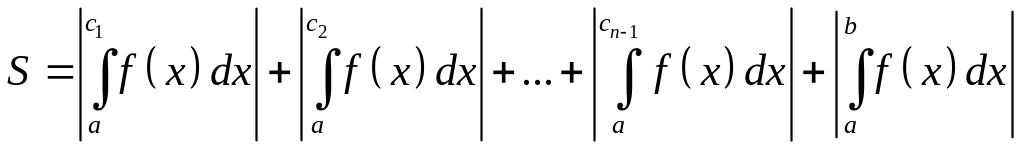
4. Двумя графиками f₁(x) и f₂(x) (f₁(x) ≥ f₂(x) для всех x), x = a, x = b

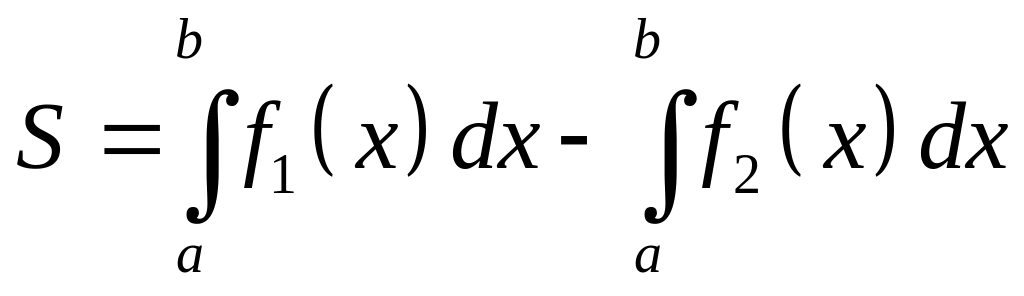
5. Двумя графиками f₁(x) и f₂(x) (общий случай), x = a, x = b

,

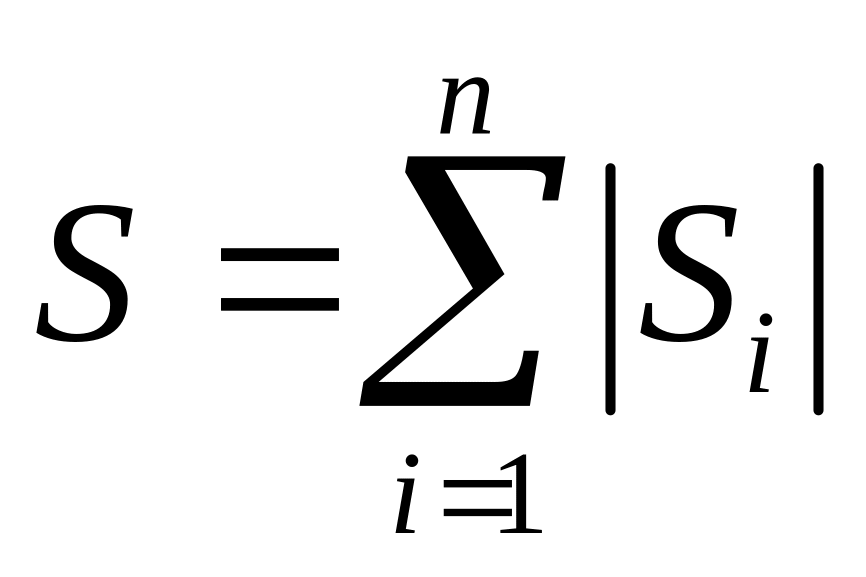где ,

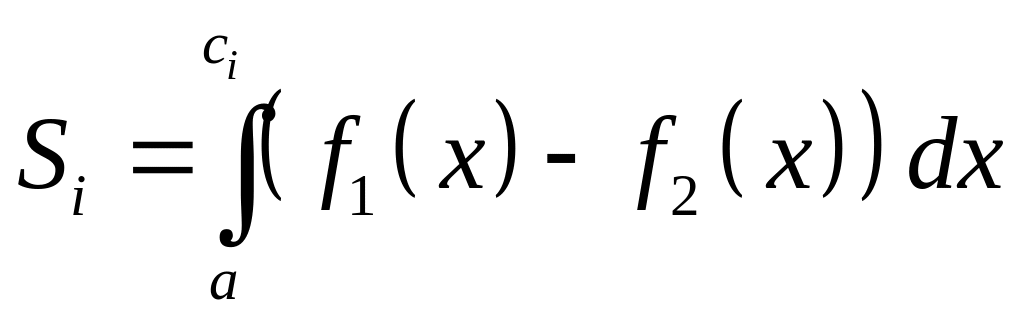где c_i – координата x точки пересечения графиков функций f₁(x) и f₂(x)

6. Простой замкнутой кривой, заданной параметрическим уравнением: