ПРОВЕРКА ГИПОТЕЗ ДЛЯ ДАННЫХ, ИЗМЕРЕННЫХ В ПОРЯДКОВОЙ ШКАЛЕ

Гипотеза об однородности двух ГС

Пусть ГС I и ГС II - две генеральные совокупности со случайным признаком Х, измеряемым в порядковой шкале.

F(x) - ФР признака Х в ГС I,

G(x) - ФР признака Х в ГС II.

Гипотеза : - распределения Х в ГС I и в ГС II совпадают.

Гипотеза : .

Пример 1. ГС I - студены – физики, ГС II - студенты – психологи.

Х – коэффициент IQ студента.

Проверка гипотезы об однородности двух гс по критерию Манна-Уитни (по критерию числа инверсий)

1. Обработка выборок.

Пусть - выборка из ГС I,

- выборка из ГС II, допустимо m ≠ n .

Условие 1. Выборки должны быть независимыми.

Условие 2. Среди чисел нет совпадающих.

Это выполнено с вероятностью 1, если Х - непрерывная случайная величина.

Проводится подсчёт числа инверсий в упорядоченных парах из элементов данных выборок: Число таких упорядоченных пар равно

Определение. Пара даёт одну инверсию, если . Если , то в паре инверсии нет. Случай пока исключается.

Вернёмся к примеру 1. Пусть получены выборки:

физики: 111, 104, 107, 90, 115, 106 m = 6,

психологи: 113, 108, 123, 122, 117, 112, 105 n = 7,

Число инверсий

Для другого порядка выборок

Проверка. (см. свойства статистики критерия).

2. Статистика критерия Манна-Уитни

= число инверсий в выборках

Свойства статистики.

1. 

2. ,

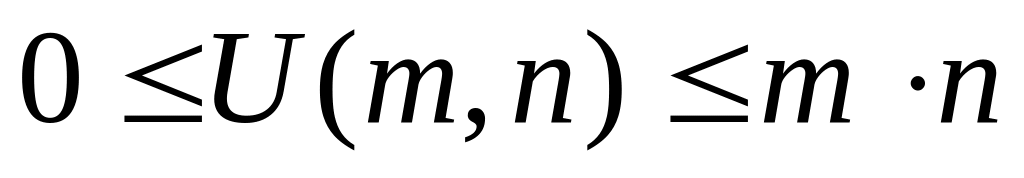
так как одна и только одна из пар обязательно даёт одну инверсию, а число пар равно

3. 

Основа статистики

1. Если гипотеза верна (законы распределения ГСI и ГСII совпадают), то для любых i, j

, (*)

поэтому, в среднем, Таким образом, при верной

2. Возьмём для простоты m = n. При верной , так как репрезентативные выборки достаточно хорошо отражают свойства генеральных совокупностей, общий вариационный ряд сделанных выборок имеет вид

При неверной (*) нарушается, например и тогда в общем вариационном ряду большая часть элементов расположится в левой половине вариационного ряда, из-за чего станет значительно меньше, чем При самой большой неоднородности распределений ГС I и ГС II общий вариационный ряд имеет вид

Следовательно, статистика критерия оценивает близость распределений ГСI и ГСII по близости её выборочного значения к mn/2.

3. По данному УЗ α при использовании двустороннего критерия Манна-Уитни по таблицам его критических значений находят левое и правое критические значения. Допустимая для принятия m и n область имеет вид

4. По выборкам находят выборочное значение статистики критерия. Если , то принимается и вероятность ошибки в принятии в точности равна α . В противном случае отклоняется.

Замечания

1. Часто в таблицах приводится только левое или правое критическое значение. Тогда недостающее критическое значение находят из равенства .

2. При больших m и n (≥ 50) критические значения статистики критерия приближённо находятся по таблицам квантилей стандартного нормального распределения. Известно, что при больших m и n

Поэтому, если - квантиль стандартного нормального распределения, то отклоняется.

3. Важно. Если в выборках имеется l совпадений, то статистику критерия считают по поправочной формуле

Если число совпадений превышает число инверсий, то пользоваться критерием Манна-Уитни не рекомендуется.

Окончание примера 1.

Возьмём α = 0,05, тогда α/2 = 0,025.

По таблицам (0,025; 6; 7) = 6, тогда (0,025; 6; 7) =36. Так как ,

принимается.

Лучше применить левосторонний критерий, так как = 8 ближе к 0 (к левому краю), чем к 21 (к середине). По таблицам (0,05; 6; 7) = 8, , поэтому принимается.

Общее правило. Если выборочное значение статистики критерия близко к середине (mn/2), то применяют двусторонний критерий, а если к краю (к 0 или к mn) – то соответствующий односторонний критерий.