
Условие
Составить транспортную задачу, воспользовавшись исходными данными линейной производственной задачи следующим образом: к каждому элементу матрицы удельных затрат прибавить единицу и принять за матрицу транспортных издержек
 ,
,
за вектор объемов
производства принять вектор объемов
ресурсов
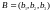 ,
а за вектор объемов потребления — вектор
,
а за вектор объемов потребления — вектор
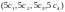 .
Найти оптимальное решение транспортной
задачи методом потенциалов. Т. е. для
каждой пары «поставщик – потребитель»
найти объемы перевозок так, чтобы:
.
Найти оптимальное решение транспортной
задачи методом потенциалов. Т. е. для
каждой пары «поставщик – потребитель»
найти объемы перевозок так, чтобы:
Мощности всех поставщиков были реализованы;
Спросы всех потребителей были удовлетворены;
Суммарные затраты на перевозку были минимальны. Решение
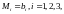
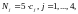

3 поставщика: M1=126, M2=84, M3=75,
4 потребителя: N1=130, N2=175, N3=90, N4=150.
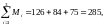

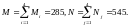
Так как N>M => добавляем фиктивного поставщика Mm+1 c мощностью N – M,
тогда
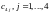 - штрафы за недопоставку.
- штрафы за недопоставку.
Заполним таблицу:
-
S\D
130
175
90
150
126
3 36
6 –
2 90
5 –
u1
84
4 –
1 84
8 –
3 –
u2
75
3 –
2 –
5 –
1 75
u3
260
0 94
0 91
0 –
0 75
u4
v1
v2
v3
v4
По заполненным клеткам имеем:
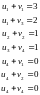
Пусть u4=0, тогда:
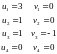
Распределение оптимально,
если по всем свободным клеткам
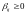 .
В нашем случае:
.
В нашем случае:
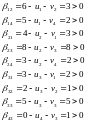
Таким образом, распределение оптимально.

Вывод
Представленное в таблице распределение оптимально, при этом затраты на перевозку равны 447 ден. ед.
VI.
Условие
Решить задачу о распределении средств между предприятиями (вариант 3.4.1(22)).
Имеются четыре предприятия, между которыми необходимо распределить 100 тыс. усл. Ед. средств. Значения прироста выпуска продукции на предприятиях в зависимости от выделенных средств Х представлены в таблице.
Х |
g1(x) |
g2(x) |
g3(x) |
g4(x) |
20 |
12 |
10 |
16 |
19 |
40 |
26 |
22 |
28 |
33 |
60 |
51 |
52 |
48 |
56 |
80 |
42 |
41 |
47 |
40 |
100 |
68 |
71 |
58 |
54 |
Составить оптимальный план распределения средств, позволяющий максимизировать общий прирост выпуска продукции.
Решение
Х |
g1(x) |
g2(x) |
g3(x) |
g4(x) |
0 |
0 |
0 |
0 |
0 |
20 |
12 |
10 |
16 |
19 |
40 |
26 |
22 |
28 |
33 |
60 |
51 |
52 |
48 |
56 |
80 |
42 |
41 |
47 |
40 |
100 |
68 |
71 |
58 |
54 |
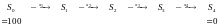
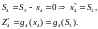
S3 |
0 |
20 |
40 |
60 |
80 |
100 |
X4* |
0 |
20 |
40 |
60 |
80 |
100 |
Z4* |
0 |
19 |
33 |
56 |
40 |
54 |
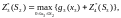

S3\X3 |
0 |
20 |
40 |
60 |
80 |
100 |
0 |
0 |
16 |
28 |
48 |
47 |
58 |
20 |
19 |
35 |
47 |
67 |
66 |
|
40 |
33 |
49 |
61 |
81 |
|
|
60 |
56 |
72 |
84 |
|
|
|
80 |
40 |
56 |
|
|
|
|
100 |
54 |
|
|
|
|
|
S2 |
0 |
20 |
40 |
60 |
80 |
100 |
X3* |
0 |
0 |
20 |
0 |
20 |
40 |
Z3* |
0 |
19 |
35 |
56 |
72 |
84 |
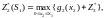
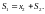
S2\X2 |
0 |
20 |
40 |
60 |
80 |
100 |
0 |
0 |
10 |
22 |
52 |
41 |
71 |
20 |
19 |
29 |
41 |
71 |
60 |
|
40 |
35 |
45 |
57 |
87 |
|
|
60 |
56 |
66 |
78 |
|
|
|
80 |
72 |
82 |
|
|
|
|
100 |
84 |
|
|
|
|
|
S1 |
0 |
20 |
40 |
60 |
80 |
100 |
X2* |
0 |
0 |
0 |
0 |
0 |
60 |
Z2* |
0 |
19 |
35 |
56 |
72 |
87 |
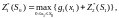

S1\X1 |
0 |
20 |
40 |
60 |
80 |
100 |
0 |
0 |
12 |
26 |
51 |
42 |
68 |
20 |
19 |
|
|
|
61 |
|
40 |
35 |
|
|
86 |
|
|
60 |
56 |
|
82 |
|
|
|
80 |
72 |
84 |
|
|
|
|
100 |
87 |
|
|
|
|
|
В итоге получаем:
Z1*=87;
при x1*=0,
S1=S0 – x1*=100-0=100 => x2*=60,
S2=S1 – x2*=100-60=40 => x3*=20,
S3=S2 – x3*=40 – 20=20=> x4*=20.
Вывод
Прибыль будет максимальной, равной 87 ден. ед., если средства между 4 предприятиями будут распределены соответственно: x1*=0, x2*=60, x3*=20, x4*=20.
